Two men and are carrying a uniform bar of length on their shoulders. The bar is held horizontally such that A gets one-fourth load. If is at one end of the bar, the distance of from that end is
The correct Answer is:C
To solve the problem, we need to analyze the situation involving two men, A and B, carrying a uniform bar of length L. The bar is held horizontally, and man A is at one end, carrying one-fourth of the total weight of the bar. We need to determine the distance of man B from man A.
1. Understanding the Load Distribution:
- Let the total weight of the bar be W.
- Man A carries W4 of the weight.
- Therefore, man B carries the remaining weight, which is W−W4=3W4.
2. Setting Up the Problem:
- Since the bar is uniform, its center of mass is located at the midpoint, which is at a distance of L2 from either end.
- Let the distance of man B from man A be X.
3. Applying the Condition of Vertical Equilibrium:
- The sum of the vertical forces must equal zero:
W4+3W4=W
- This confirms that the forces are balanced.
4. Applying the Condition of Rotational Equilibrium:
- We will take moments about point A to ensure the bar does not rotate. The moment due to the weight at the center of the bar (acting at L2) and the moment due to the weight carried by man B (acting at distance X) must balance.
- The clockwise moment due to the weight W at the center is:
W×L2
- The anti-clockwise moment due to the weight carried by man B is:
3W4×X
5. Setting Up the Moment Equation:
- Setting the sum of moments about point A to zero gives:
W×L2=3W4×X
6. Solving for X:
- Cancel W from both sides (assuming W≠0):
L2=34X
- Rearranging gives:
X=L2×43=2L3
7. Conclusion:
- The distance of man B from man A is 2L3.
Final Answer:
The distance of man B from man A is 2L3.
- Let the total weight of the bar be W.
- Man A carries W4 of the weight.
- Therefore, man B carries the remaining weight, which is W−W4=3W4.
- Since the bar is uniform, its center of mass is located at the midpoint, which is at a distance of L2 from either end.
- Let the distance of man B from man A be X.
- The sum of the vertical forces must equal zero:
W4+3W4=W
- This confirms that the forces are balanced.
- We will take moments about point A to ensure the bar does not rotate. The moment due to the weight at the center of the bar (acting at L2) and the moment due to the weight carried by man B (acting at distance X) must balance.
- The clockwise moment due to the weight W at the center is:
W×L2
- The anti-clockwise moment due to the weight carried by man B is:
3W4×X
- Setting the sum of moments about point A to zero gives:
W×L2=3W4×X
- Cancel W from both sides (assuming W≠0):
L2=34X
- Rearranging gives:
X=L2×43=2L3
- The distance of man B from man A is 2L3.
The distance of man B from man A is 2L3.
Topper's Solved these Questions
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Level-v(Single answer)
Explore 23 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Multiple answer
Explore 6 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
- MAGNETISMBook:NARAYNAChapter:MAGNETISMExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
Two men are carrying a uniform bar of length L on their shoulders.The bar is held horizontally such that younger man gets (14)th of load.Suppose the younger man is at one end of the bar.The distance of other man from the second end is ?
View Solutionthere is a bar of length a cm whose one end is on origin and other end is on the X-axis find Co ordinate of both the ends of the bar
View Solution
Knowledge Check
Two men are carrying a uniform bar of length L on their shoulders.The bar is held horizontally such that younger man gets (14)th of load.Suppose the younger man is at one end of the bar.The distance of other man from the second end is ?
AL3BL4C2L3D3L4A boy and a man carry a uniform rod of length L horizontally in such a way that the boy gets (14)th of the load. If the boy is at one end of the rod, the distance of the man from the other end is:
AL3BL4C2L3D3L4A horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to
AWBW2C3W4DW4
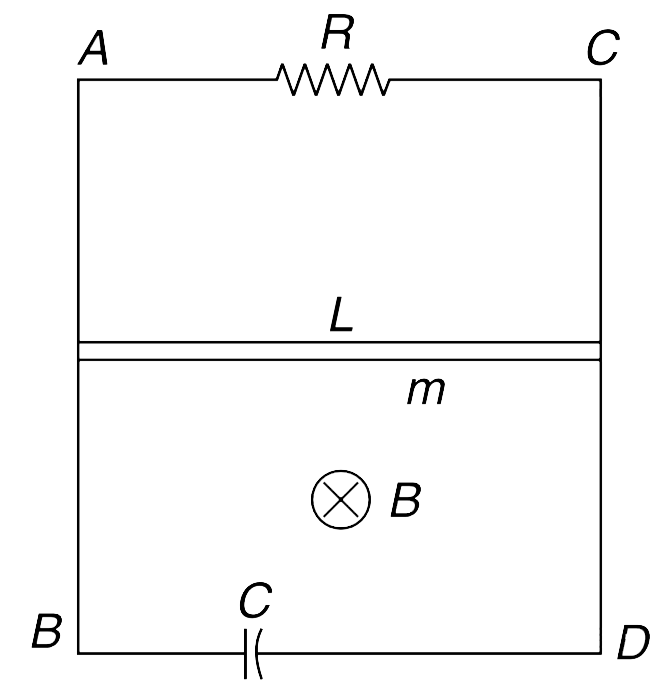
Two long fixed parallel vertical conducting rails AB and CD are separated by a distance L. They are connected by resistance R and a capacitance C at two ends as shown in the figure. There is a uniform magnetic field B directed horizon- tally into the plane of the figure. A horizontal metallic bar of length L and mass m can slide without friction along the rails. The bar is released from rest at t = 0. Neglect resistance of bar and rails and also neglect the self inductance of the loop.
(a) Find the maximum speed acquired by the bar after it is released.
(b) Find the speed of the bar as a function of time t.
View SolutionA bar of length 20 units moves with its ends on two fixed straight lines at right angles. A point P marked on the bar ata distance of 8 units from one end describes a conic whose eccentricity is
View SolutionA uniform bar of square cross-section is lying along a frictionless horizontal surface. A horizontal force is applied to pull it from one of its ends then

View SolutionWhen one end of an iron bar is placed near a compass:
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'l' from that end is
View Solution

