A metal bar 70cm long and 4.00kg in mass is supported on two knife edges placed 10cm from each end. A 6.00kg weight is suspended at 30cm from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
To solve the problem of finding the reactions at the knife edges supporting a metal bar with a suspended weight, we can follow these steps:
Step 1: Understand the Setup
- The metal bar is 70 cm long and has a mass of 4.00 kg.
- The knife edges are placed 10 cm from each end of the bar.
- A 6.00 kg weight is suspended at a distance of 30 cm from one end of the bar.
Step 2: Identify Forces Acting on the System
- The weight of the bar (W_bar) can be calculated as:
Wbar=mbar⋅g=4.00kg⋅9.8m/s2=39.2N
- The weight of the suspended mass (W_weight) is:
Wweight=mweight⋅g=6.00kg⋅9.8m/s2=58.8N
Step 3: Set Up the Free Body Diagram (FBD)
- Let R1 be the reaction force at the left knife edge and R2 be the reaction force at the right knife edge.
- The total downward forces are Wbar+Wweight=39.2N+58.8N=98.0N.
Step 4: Apply the Equilibrium Condition for Vertical Forces
According to the equilibrium condition:
R1+R2=Wbar+Wweight
Substituting the values:
R1+R2=98.0N(Equation 1)
Step 5: Calculate the Torque About One of the Knife Edges
To find the reactions, we can take moments about one of the knife edges. Let's take moments about the left knife edge (where R1 acts):
- The distance from the left edge to the center of the bar (where the weight acts) is 35cm−10cm=25cm.
- The distance from the left edge to the point where the 6 kg weight is suspended is 30cm−10cm=20cm.
Setting up the torque equation (taking counter-clockwise as positive):
Wweight⋅20cm+Wbar⋅25cm=R2⋅50cm
Substituting the weights:
58.8N⋅20cm+39.2N⋅25cm=R2⋅50cm
Calculating the left side:
1176+980=R2⋅50
2156=R2⋅50
R2=215650=43.12N(Equation 2)
Step 6: Substitute R2 Back into Equation 1
Now substitute R2 back into Equation 1 to find R1:
R1+43.12=98.0
R1=98.0−43.12=54.88N
Final Answers
- R1=54.88N
- R2=43.12N
- The metal bar is 70 cm long and has a mass of 4.00 kg.
- The knife edges are placed 10 cm from each end of the bar.
- A 6.00 kg weight is suspended at a distance of 30 cm from one end of the bar.
- The weight of the bar (W_bar) can be calculated as:
Wbar=mbar⋅g=4.00kg⋅9.8m/s2=39.2N
- The weight of the suspended mass (W_weight) is:
Wweight=mweight⋅g=6.00kg⋅9.8m/s2=58.8N
- Let R1 be the reaction force at the left knife edge and R2 be the reaction force at the right knife edge.
- The total downward forces are Wbar+Wweight=39.2N+58.8N=98.0N.
According to the equilibrium condition:
R1+R2=Wbar+Wweight
Substituting the values:
R1+R2=98.0N(Equation 1)
To find the reactions, we can take moments about one of the knife edges. Let's take moments about the left knife edge (where R1 acts):
- The distance from the left edge to the center of the bar (where the weight acts) is 35cm−10cm=25cm.
- The distance from the left edge to the point where the 6 kg weight is suspended is 30cm−10cm=20cm.
Wweight⋅20cm+Wbar⋅25cm=R2⋅50cm
Substituting the weights:
58.8N⋅20cm+39.2N⋅25cm=R2⋅50cm
Calculating the left side:
1176+980=R2⋅50
2156=R2⋅50
R2=215650=43.12N(Equation 2)
Now substitute R2 back into Equation 1 to find R1:
R1+43.12=98.0
R1=98.0−43.12=54.88N
- R1=54.88N
- R2=43.12N
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE B
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE C
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE A
2 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A metal rod of length 50cm having mass 2kg is supported on two edges placed 10cm from each end. A 3kg load is suspended at 20cm from one end. Find the reactions at the edges (take g=10m/s2)
View SolutionTwo cubes each of 10cm edge are joined end to end. Find the surface area of the resulting cuboid.
View Solution
Knowledge Check
A uniform rod of length 1m mass 4kg is supports on two knife-edges placed 10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
A60 N, 40 NB75 N, 25 NC65 N, 35 ND55 N, 45 NA uniform rod is 4m long and weights 10kg. If it is supported on a kinetic edge at one meter from the end, what weight placed at that end keeps the rod horizontal.
A8kgB10kgC12kgD15kgOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
Aw1+w2ABw1−w2AC(w12)+w2AD(w22)+w1A
One end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionA diving board 3.00m long is supported at a point 1.00m from the end and a diver weighing 500N stands at the free end. The diving board is of uniform cross section and weighs 280N. Find.
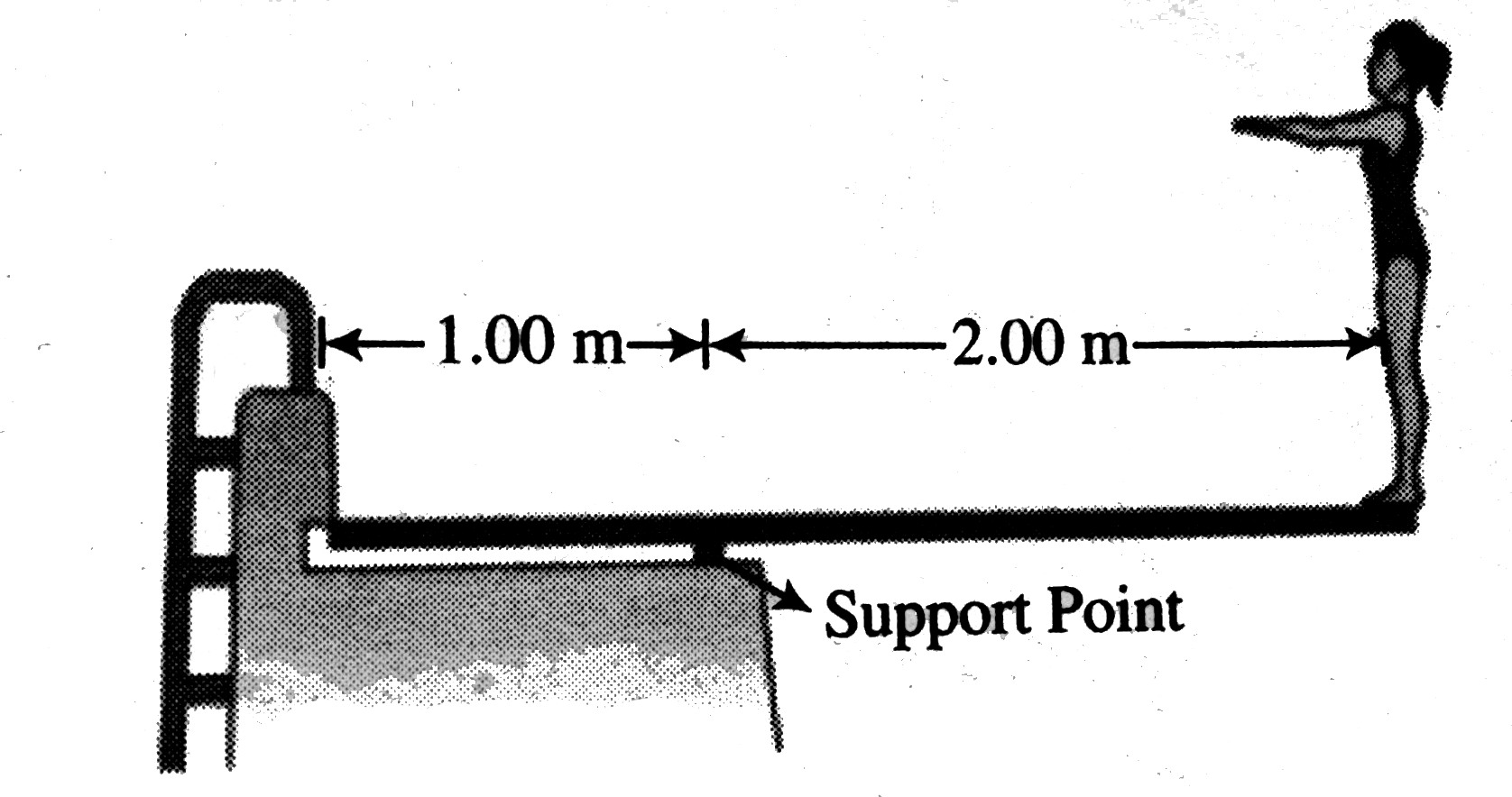
The force at the support point
View SolutionA diving board 3.00m long is supported at a point 1.00m from the end and a diver weighing 500N stands at the free end. The diving board is of uniform cross section and weighs 280N. Find.

The force at the end that is held down.
View SolutionA swimming pool, 30 m long has a depth of water of 80 cm at one end and 2.4 m the other end. Find the area of the vertical cross-section of the pool along the length.
View SolutionA rigid massless rod AB of length 1m is placed horizontally on two rigid supports at its ends as showm in figure. A weight 10N is hung from a point C at a distance 30cm from A. Find the reactions at the supports A and B respectively.
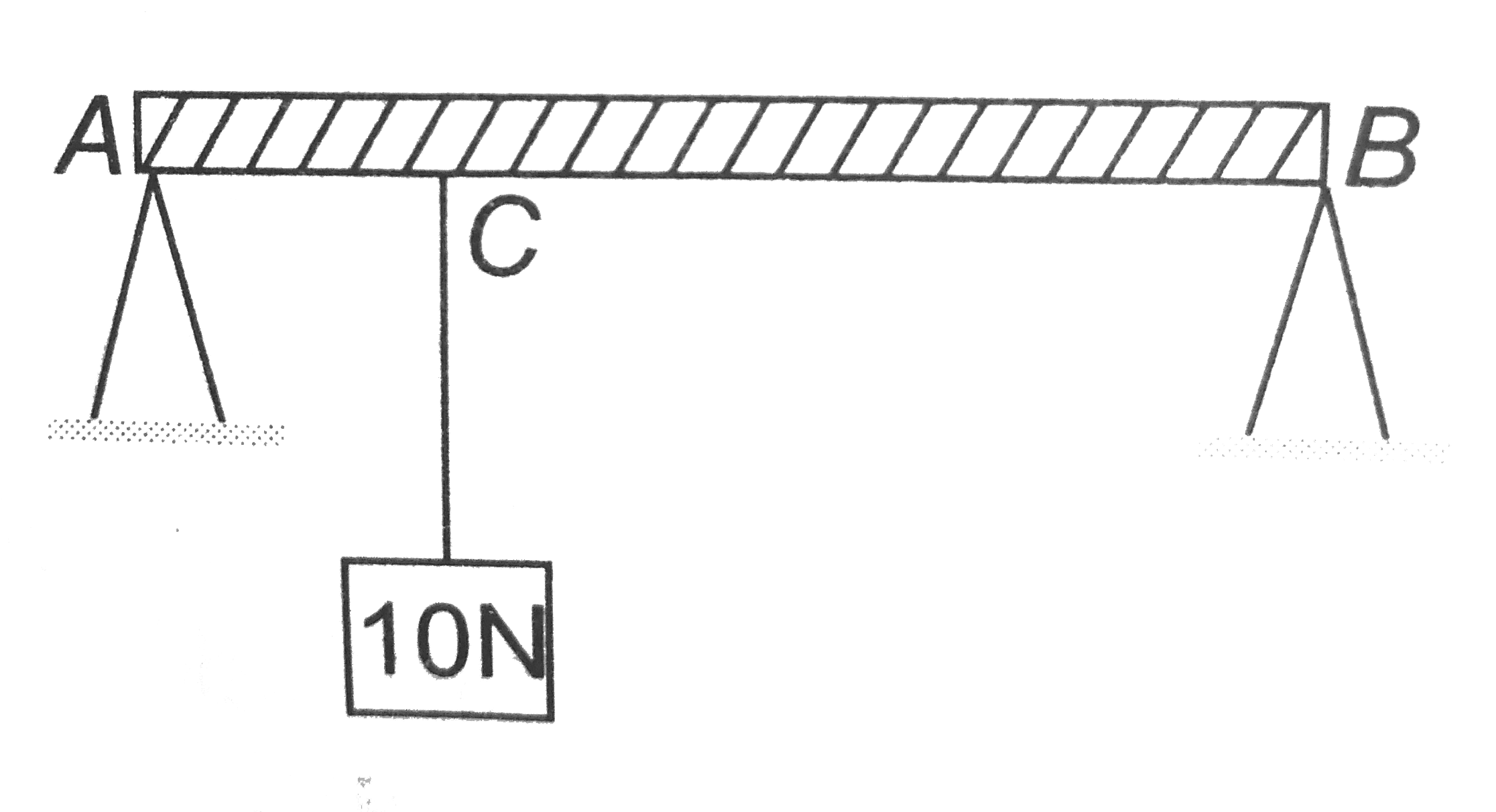 .
.
View Solution