Find the moment of inertia of a rectangular bar magent about an axis passing through its centre and parallel to its thickness. Mass of magent is 100g, its length is 12cm, breadth is 3cm and thickness is 2cm.
Here, I=?,m=100g,
l=12cm,b=3cm,t=2cm
The axis shown in the Fig. is parallel to thickness of rentangular bar.
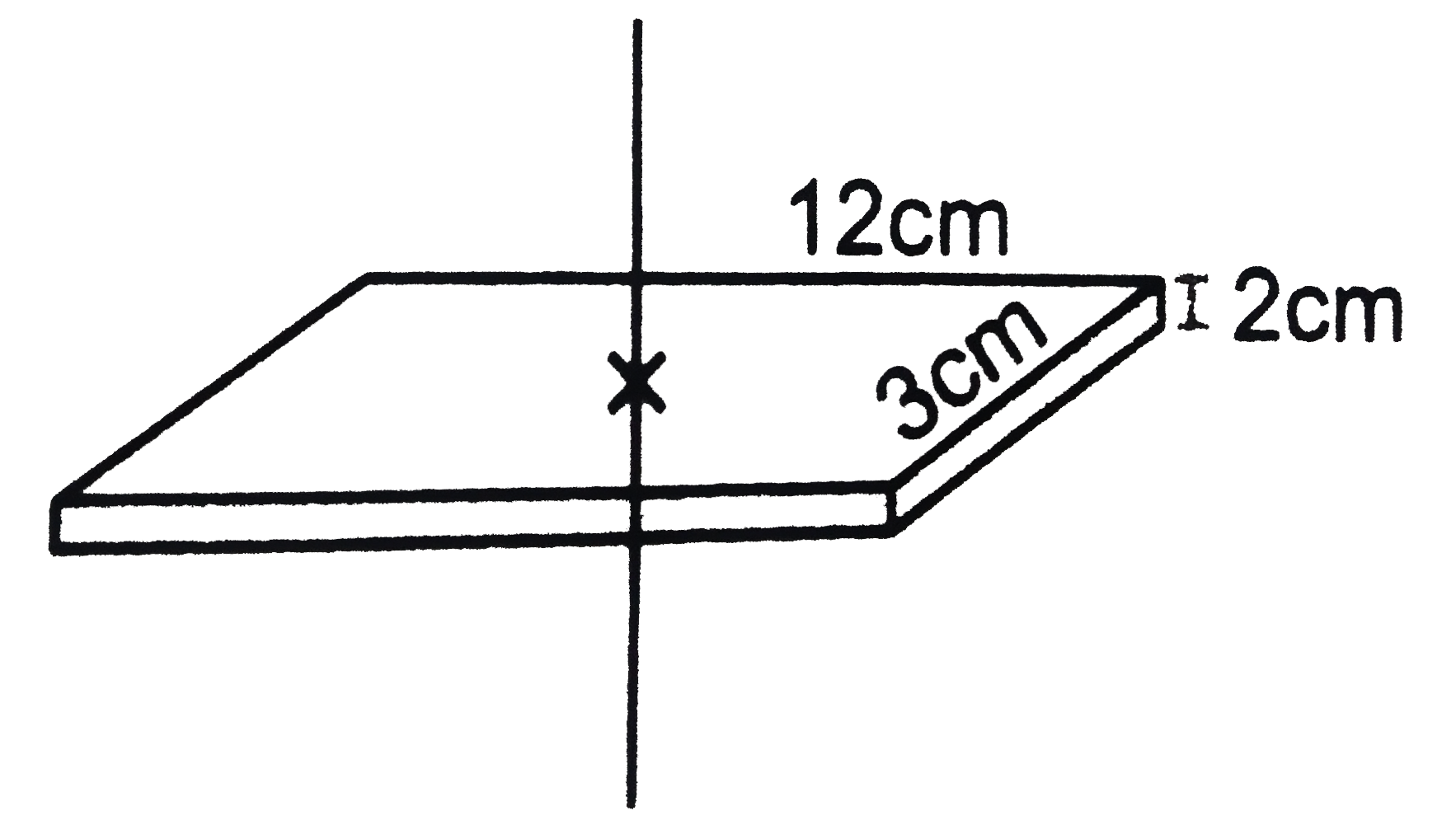
I=m(l2+b212)=100(122+3212)
=100×15312=1275gcm2
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE B
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE C
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE A
Explore 2 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Calculate the moment of inertia of a rectangular bar about an axis passing through the centre and perpendicular to its length. Mass of bar is 0.2 kg and length is 10 cm
View SolutionThe moment of inertia of uniform rectangular plate about an axis passing through its mid-point and parallel to its length l is (b = breadth of rectangular plate)
View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctThe moment of inertia of a ring of mass 5 gram and radius 1 cm about and axis passing through its edge and parallel to its natural axis is
A5g−cm2B2.5 g - cm2C20 g - cm2D10 g - cm2A cylinder of 500 g and radius 10 cm has moment of inertia about an axis passing through its centre and parallel to its length is
A2.5×10−3kgm2B2×10−3kgm2C5×10−3kgm2D3.5×10−3kgm2
Calculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionMoment of inertia of a ring of mass m = 3 gm and radius r = 1 cm about an axis passing through its edge and parallel to its natural axis is
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an angle α is

View Solution

