Two identical uniform rods of length l are joined to from L shaped frame, as shown is Fig. Locate the centre of mass of the frame.
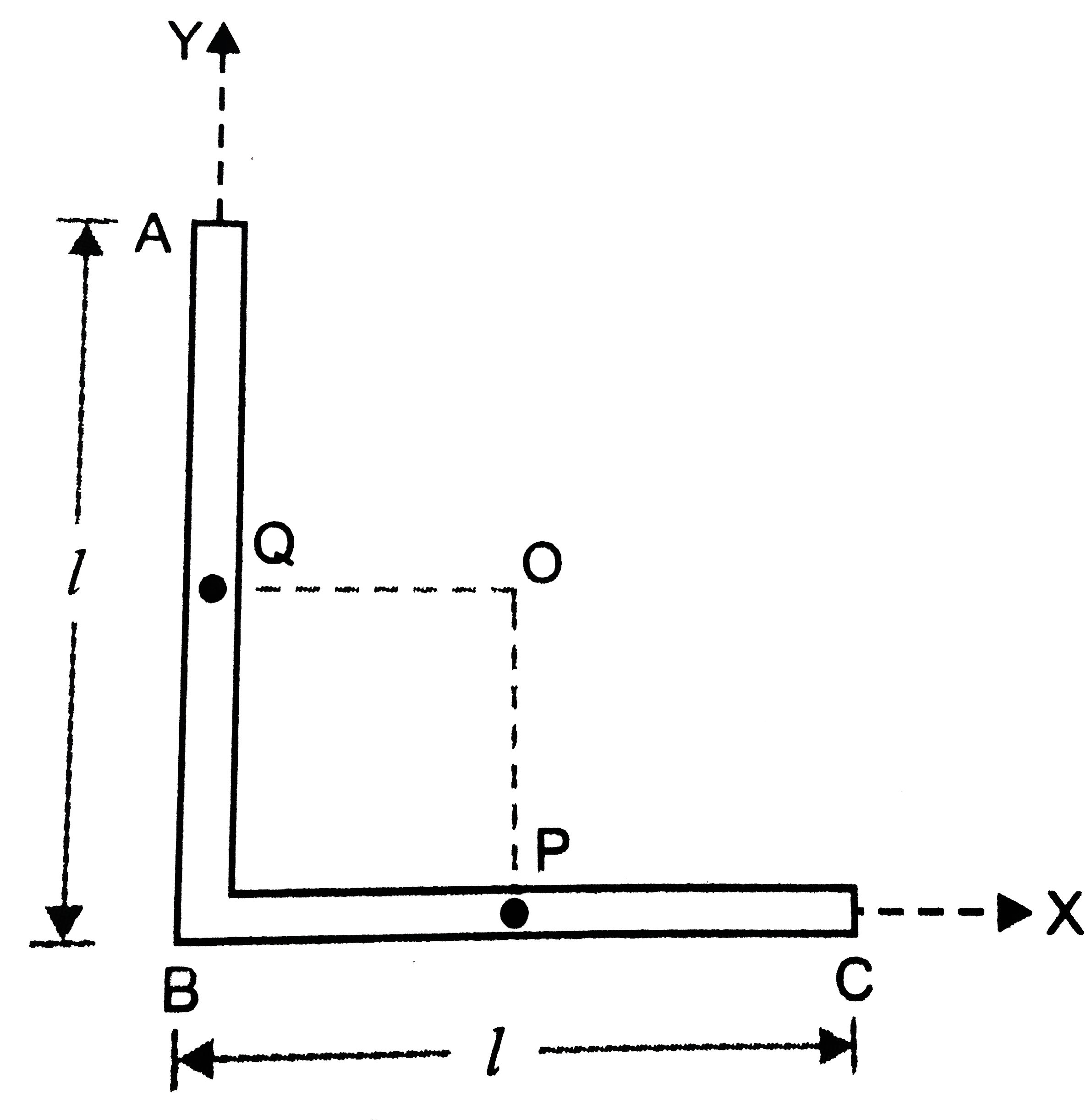
Let m be the mass of each rod. In Fig. B is taken as origin. BC is X-axis and BA is Y-axis. As the rods are uniform, their individual centre of mass must be lying at there respective centres, say P and Q. Thus the system is equivalent to two point masses m each, at P(l/2,0) and Q(0,l/2)
∴xcm=m×l/2+m×0m+m=l/4
and ycm=m×0+m×l/2m+m=l/4
Hence centre of mass of the system is at O(l/4,l/4).
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES
Explore 62 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SOLVED EXAMPLES TYPE B
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Two identical uniform rods AB and CD, each of length L are jointed to form a T-shaped frame as sown in figure. Locate the centre of mass of the frame. The centre of mass of a uniform rod is at the middle point of the rod.

View SolutionTwo uniform identicla rods each of mass M and length l are joined to form a cross as shown in figure. Find the momet of inertia of the cross about a bisector as shown doted in the figure

View Solution
Knowledge Check
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
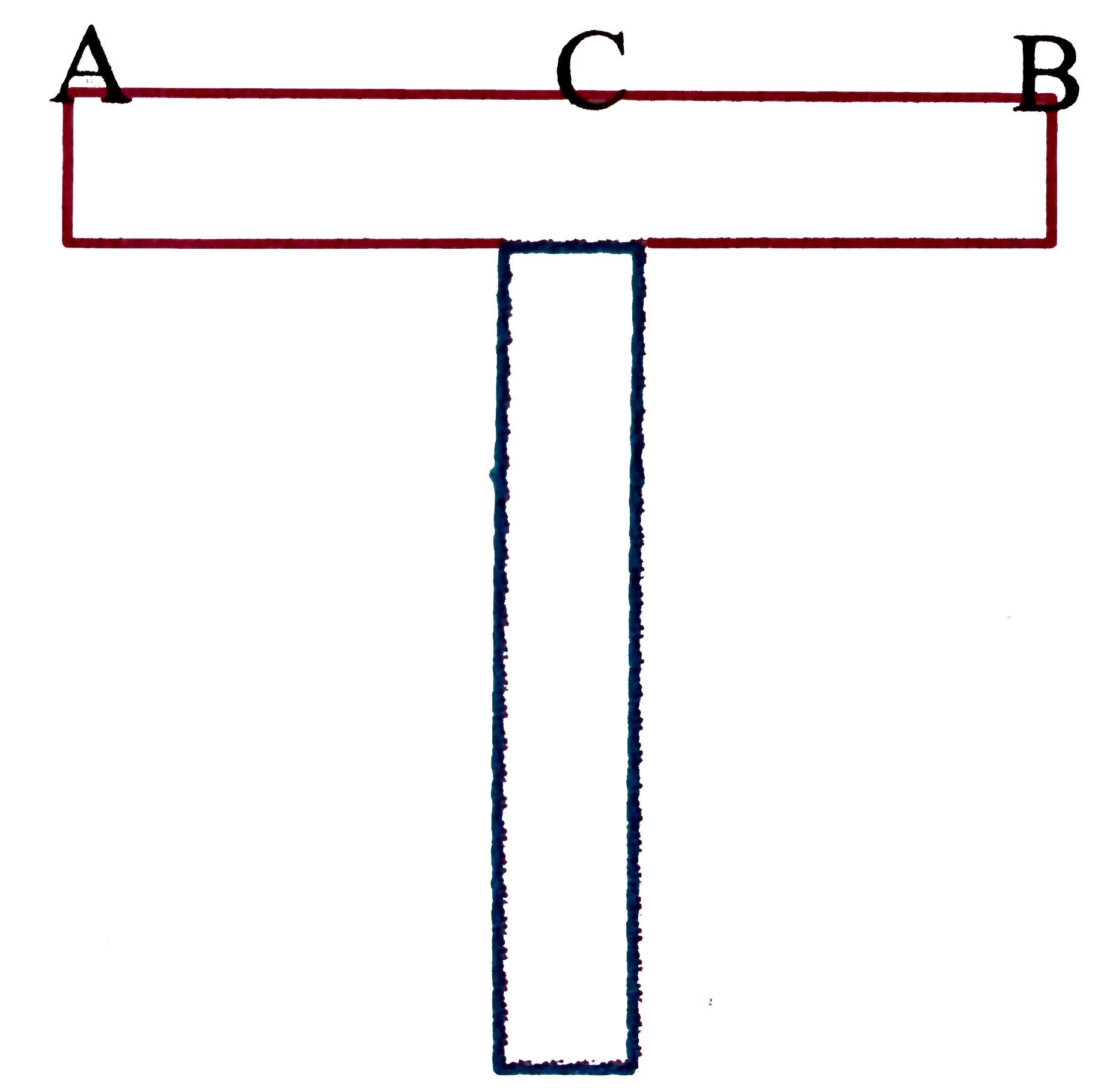 A0BL/4C3L/4DL
A0BL/4C3L/4DLA uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-
 Al/2Bl√34Cl√38DNone of these
Al/2Bl√34Cl√38DNone of theseA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionA rod of length 2l is bent as shown in figure. Coordinates of centre of mass are
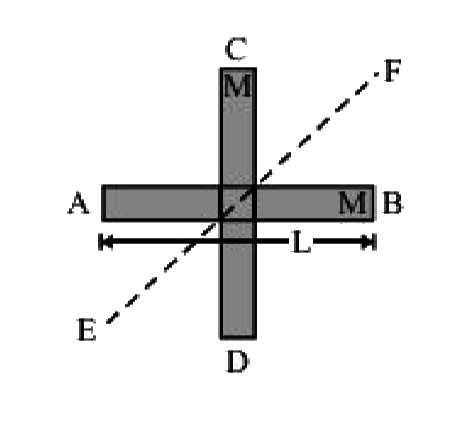
View SolutionTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form as cross as shown. The monent of inertia of the cross about a bisector line EF is

View SolutionTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertial about
View Solution

