Find the out the moment of inertia of a ring having uniform mass distribution of mass $M$ and radius $R$ about an axis which is tangent ot the ring and ( $a$ ) in the plane of the ring ( $b$ ). perpendicular to the plane of the ring.

Video Solution

Text Solution

Verified by Experts

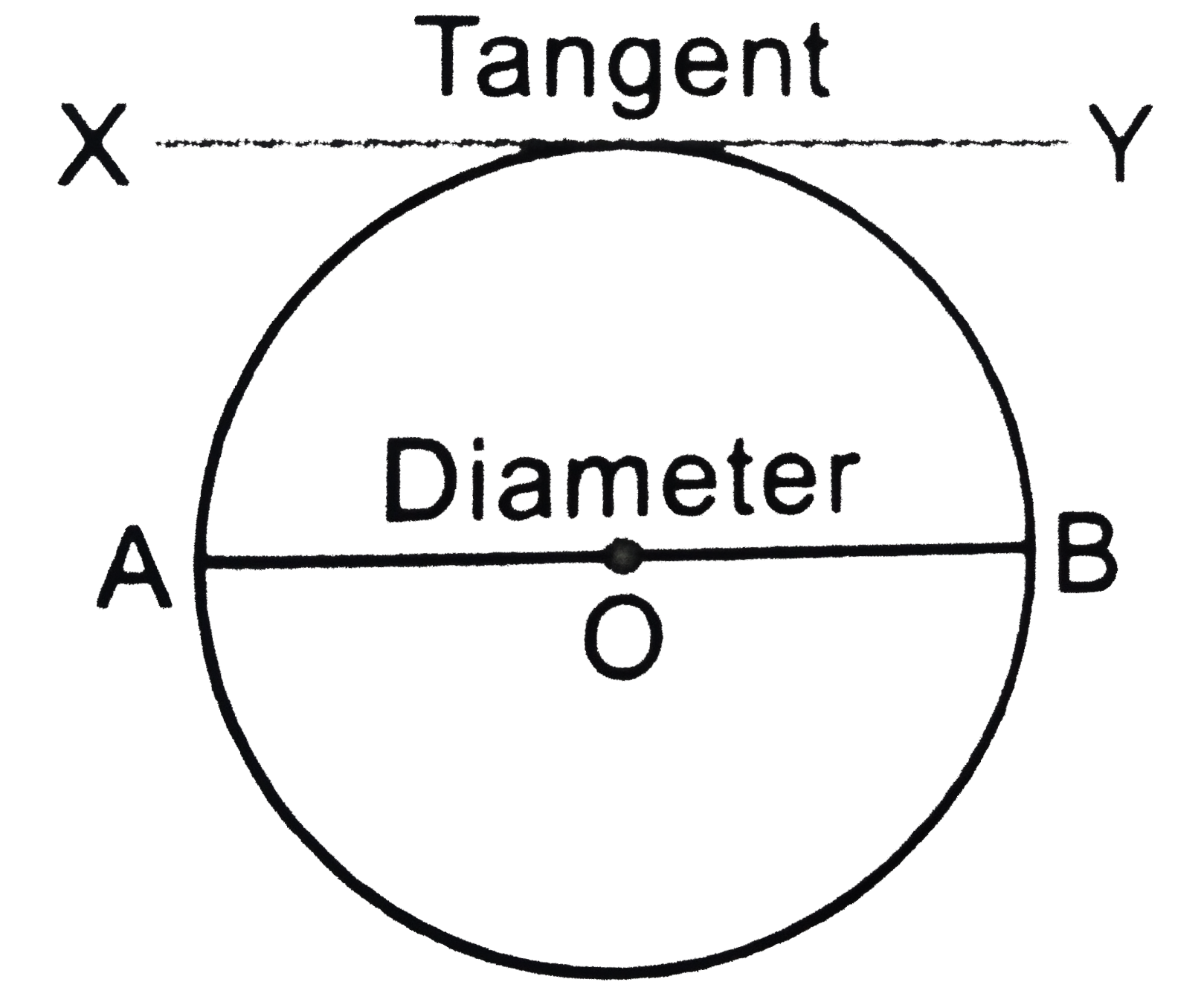
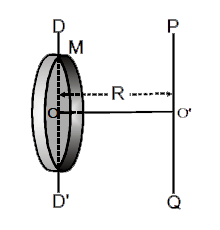
Moment of inertia of a circular ring of mass $M$ and radius $R$ about the diameter $A B$ , Fig.

$I_{A B} = \frac{M R^{2}}{2}$
The given axis is $X Y$ , tangent to the ring in the plane of ring and parallel to its diameter $A B$ . using the theorem of parallel axes,
$I_{X Y} = I_{A B} + M R^{2} = \frac{1}{2} M R^{2} + M R^{2} = \frac{3}{2} M R^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $\frac{5}{2} M R^{2}$
B $\frac{3}{2} M R^{2}$
C $\frac{1}{2} M R^{2}$
D $M R^{2}$
Question 2 - Select One
Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A $M R^{2}$
B $\frac{1}{2} M R^{2}$
C $\frac{3}{2} M R^{2}$
D $\frac{7}{2} M R^{2}$
Question 3 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A $1 / 2 M R^{2}$
B $M R^{2}$
C $1 / 4 M R^{2}$
D $3 / 4 M R^{2}$

PRADEEP-SYSTEMS OF PARTICLES AND ROTATIONAL MOTION-SOLVED EXAMPLES

Home
Ask Doubt
Profile