A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

YCM=−R15
YCM=−R40
YCM=−R30
YCM=−R20
The correct Answer is:B
Step by step video, text & image solution for A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
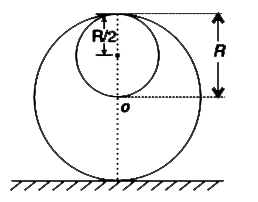
A spherical cavity of radiusR2 is removed from a solid sphere of radius R as shown in fig. The sphere is placed on a rough horizontal surface as shown. The sphere is given a gentle push. Friction is large enough to prevent slippage. Prove that the sphere perform SHM and find the time period.
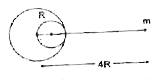
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
View Solution
Knowledge Check
A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 Axcm=−R/15Bycm=−R40Czcm=zeroDNone of these
Axcm=−R/15Bycm=−R40Czcm=zeroDNone of theseA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
Amg2B3mg8Cmg16Dnone of these
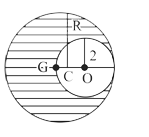
As shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
View SolutionA spherical cavity of radius R2 is made in a sphere of radius R and mass M. The centre of the cavity is at a distance R2 from the centre of the sphere. The intensity of gravitational field at the centre of cavity is GMnR2. Find n.
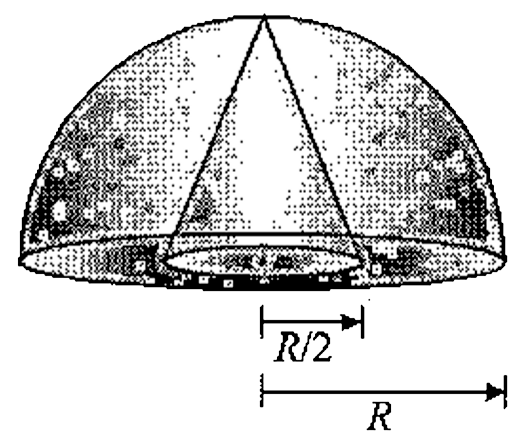
View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2r. A charge 9 is kept at the centre of cavity as shown in the figure. Find the magnitude of the total electric field at(4r 0). у r (0 0) х 9 2r
View Solution

