A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
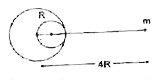
PEnet=PEdue to entirc sphere−PEdue to removed portion
PEnet=−GMm4R−[−GMm4R−(R/2)] but M.=M8(∴M∝R3)M.=(M/43πR3)43π(R2)3=M8
PEnet=−6GMm28R
Topper's Solved these Questions
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Matrix match type
2 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Exercise
11 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Assertion & Reasoning type
1 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
Similar Questions
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
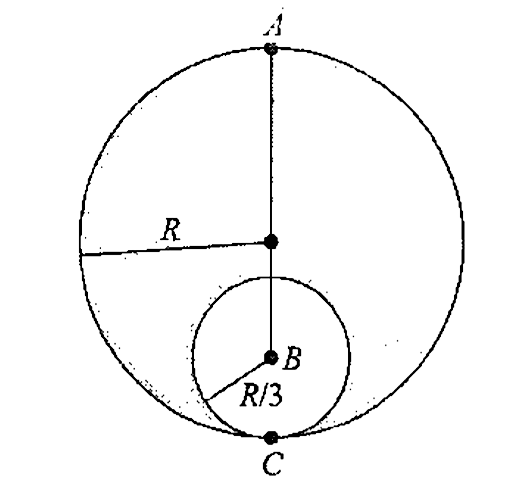 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is
 Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of these
Anon - uniformBtowards the center of the cavityCdirectly proportional to aDAll of theseA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmR
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View SolutionA mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
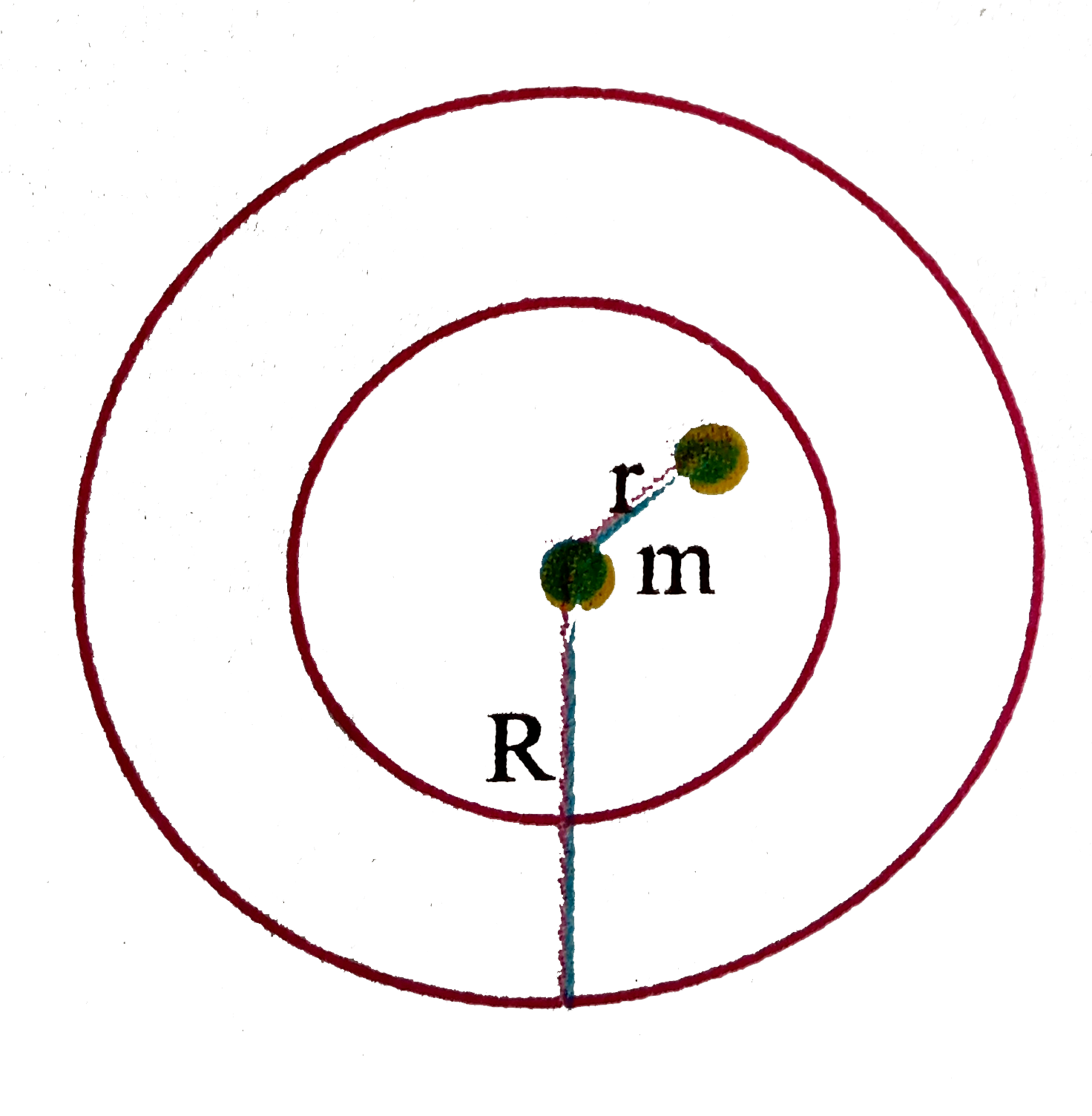
View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V=0atr=∞, the potential at (G = gravitational constatn)

View Solution
