A uniform metre rod is bent into shape with the bent arms at to each other. The distance of the centre of mass from the bent point is
The correct Answer is:A
To find the distance of the center of mass from the bent point of a uniform metre rod bent into an 'L' shape, we can follow these steps:
Step 1: Understand the Configuration
The rod is bent at a right angle, forming two equal segments. Since the total length of the rod is 1 metre, each arm of the 'L' shape will be L2=12 metre.
Step 2: Assign Masses
Let the total mass of the rod be M. When bent into an 'L' shape, each arm will have a mass of M2.
Step 3: Set the Coordinate System
We will set the bent point (the corner of the 'L') as the origin (0,0). The first arm (horizontal) will extend along the x-axis, and the second arm (vertical) will extend along the y-axis.
Step 4: Calculate the Center of Mass in the X-Direction
For the horizontal arm:
- Mass M1=M2
- The center of mass of this arm is at (L4,0) because it is halfway along the arm.
For the vertical arm:
- Mass M2=M2
- The center of mass of this arm is at (0,L4).
Using the formula for the center of mass in the x-direction:
XCM=M1X1+M2X2M1+M2
Substituting the values:
XCM=(M2⋅L4)+(M2⋅0)M2+M2=ML8M=L8
Step 5: Calculate the Center of Mass in the Y-Direction
Using the formula for the center of mass in the y-direction:
YCM=M1Y1+M2Y2M1+M2
Substituting the values:
YCM=(M2⋅0)+(M2⋅L4)M2+M2=ML8M=L8
Step 6: Calculate the Distance from the Bent Point
Now, we have the coordinates of the center of mass:
(XCM,YCM)=(L8,L8)
To find the distance D from the bent point (origin) to the center of mass, we use the distance formula:
D=√X2CM+Y2CM
Substituting the values:
D=√(L8)2+(L8)2=√L264+L264=√2L264=√L232=L4√2
Final Answer
The distance of the center of mass from the bent point is:
L4√2 metres
The rod is bent at a right angle, forming two equal segments. Since the total length of the rod is 1 metre, each arm of the 'L' shape will be L2=12 metre.
Let the total mass of the rod be M. When bent into an 'L' shape, each arm will have a mass of M2.
We will set the bent point (the corner of the 'L') as the origin (0,0). The first arm (horizontal) will extend along the x-axis, and the second arm (vertical) will extend along the y-axis.
For the horizontal arm:
- Mass M1=M2
- The center of mass of this arm is at (L4,0) because it is halfway along the arm.
- Mass M2=M2
- The center of mass of this arm is at (0,L4).
XCM=M1X1+M2X2M1+M2
Substituting the values:
XCM=(M2⋅L4)+(M2⋅0)M2+M2=ML8M=L8
Using the formula for the center of mass in the y-direction:
YCM=M1Y1+M2Y2M1+M2
Substituting the values:
YCM=(M2⋅0)+(M2⋅L4)M2+M2=ML8M=L8
Now, we have the coordinates of the center of mass:
(XCM,YCM)=(L8,L8)
To find the distance D from the bent point (origin) to the center of mass, we use the distance formula:
D=√X2CM+Y2CM
Substituting the values:
D=√(L8)2+(L8)2=√L264+L264=√2L264=√L232=L4√2
The distance of the center of mass from the bent point is:
L4√2 metres
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform wire is bent into the form of a rectangle of length L and width W. The coordinates of its centre of mass from a corner are
View SolutionA thick uniform wire is bent into the shape of the letter "U" as shown. Which point indicates the location of the center of mass of this wire ? A is the midpoint of the line joining mid points of two parallel sides of 'U' shaped wire.
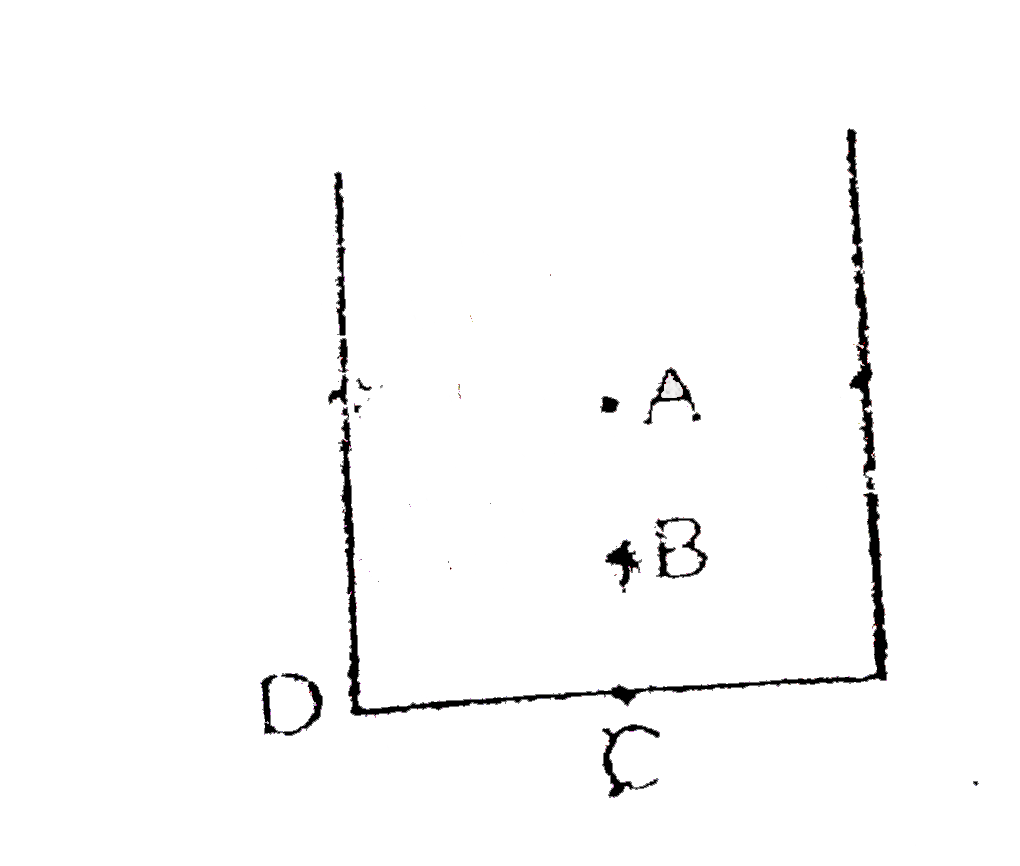
View Solution
Knowledge Check
A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)A uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-
 Al/2Bl√34Cl√38DNone of these
Al/2Bl√34Cl√38DNone of theseA uniform rod o length one meter is bent at its midpoint to make 90∘. The distance of centre of mass from the centre of rod is (in cm)
A20.2B13.4C15D17.6
A uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
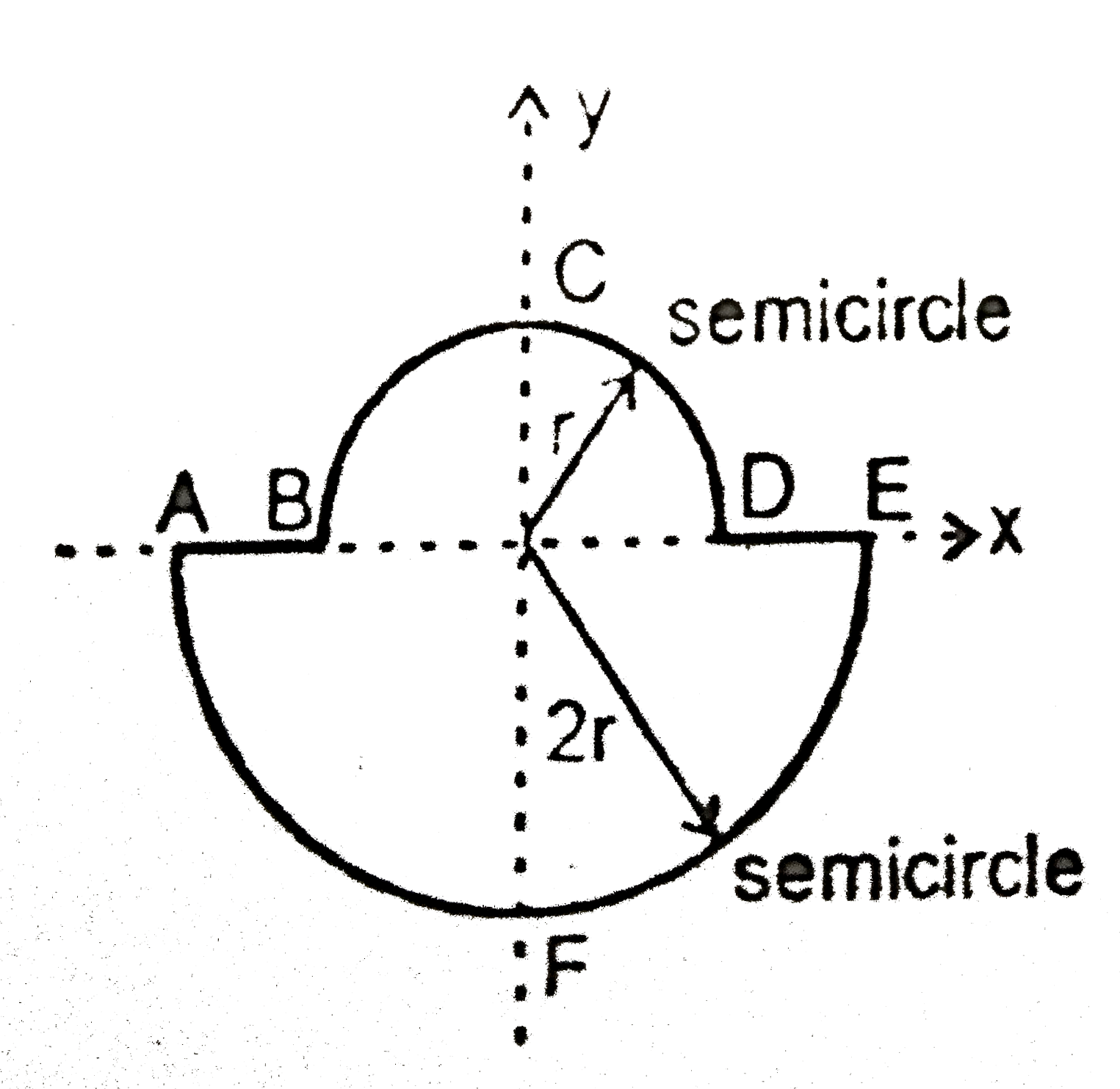
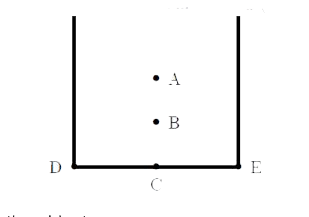
View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
View SolutionA uniform metal rod of length 1m is bent at 90∘, so as to form two arms of equal length. The centre of mass of this bent rod is
View SolutionA sector cut from a uniform disk of radius 12cm and a uniform rod of the same mass bent into shape of an arc are arranged facing each other as shown in the figure. If center of mass of the combination is at the origin, what is the raius of the arc?
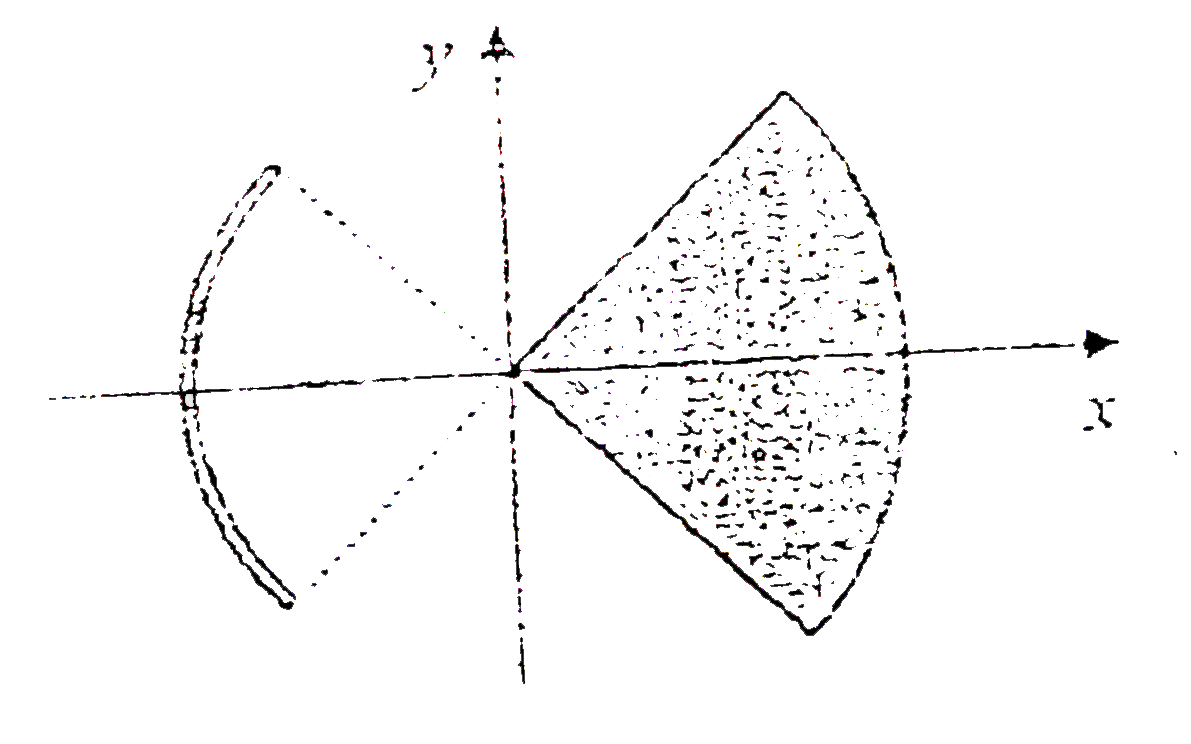
View SolutionTwo identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
View Solution
