A uniform wire is bent into the form of a rectangle of length L and width W. The coordinates of its centre of mass from a corner are
(0,0)
(L2,W)
(L,W2)
(L2,W2)
The correct Answer is:D
To find the coordinates of the center of mass of a uniform wire bent into the shape of a rectangle with length L and width W, we can follow these steps:
Step 1: Understand the Geometry
The rectangle has a length L and a width W. We need to determine the coordinates of its center of mass from one of its corners, which we can assume to be the origin (0, 0).
Step 2: Identify the Center of Mass Formula
For a uniform wire, the center of mass (CM) can be found using the formula:
Xcm=∫xdm∫dm
Ycm=∫ydm∫dm
Where dm is the mass element of the wire.
Step 3: Calculate the Mass Element
Since the wire is uniform, we can express the mass per unit length (linear mass density) as:
λ=ML+2W
where M is the total mass of the wire.
Step 4: Calculate the X Coordinate of the Center of Mass
1. The wire consists of four segments: two lengths L and two widths W.
2. The x-coordinates of the segments are:
- For the bottom segment (length L): x=L2
- For the top segment (length L): x=L2
- For the left segment (width W): x=0
- For the right segment (width W): x=L
3. The contribution to the x-coordinate from each segment:
- Bottom segment: L2⋅L
- Top segment: L2⋅L
- Left segment: 0⋅W
- Right segment: L⋅W
4. The total x-coordinate of the center of mass:
Xcm=(L⋅L2)+(L⋅L2)+(W⋅0)+(W⋅L)L+2W
Xcm=L2+WLL+2W=L2
Step 5: Calculate the Y Coordinate of the Center of Mass
1. The y-coordinates of the segments are:
- For the bottom segment (length L): y=0
- For the top segment (length L): y=W
- For the left segment (width W): y=W2
- For the right segment (width W): y=W2
2. The contribution to the y-coordinate from each segment:
- Bottom segment: 0⋅L
- Top segment: W⋅L
- Left segment: W2⋅W
- Right segment: W2⋅W
3. The total y-coordinate of the center of mass:
Ycm=(0⋅L)+(W⋅L)+(W2⋅W)+(W2⋅W)L+2W
Ycm=WL+W2L+2W=W2
Final Result
The coordinates of the center of mass from the corner of the rectangle are:
(L2,W2)
The rectangle has a length L and a width W. We need to determine the coordinates of its center of mass from one of its corners, which we can assume to be the origin (0, 0).
For a uniform wire, the center of mass (CM) can be found using the formula:
Xcm=∫xdm∫dm
Ycm=∫ydm∫dm
Where dm is the mass element of the wire.
Since the wire is uniform, we can express the mass per unit length (linear mass density) as:
λ=ML+2W
where M is the total mass of the wire.
1. The wire consists of four segments: two lengths L and two widths W.
2. The x-coordinates of the segments are:
- For the bottom segment (length L): x=L2
- For the top segment (length L): x=L2
- For the left segment (width W): x=0
- For the right segment (width W): x=L
- Bottom segment: L2⋅L
- Top segment: L2⋅L
- Left segment: 0⋅W
- Right segment: L⋅W
Xcm=(L⋅L2)+(L⋅L2)+(W⋅0)+(W⋅L)L+2W
Xcm=L2+WLL+2W=L2
1. The y-coordinates of the segments are:
- For the bottom segment (length L): y=0
- For the top segment (length L): y=W
- For the left segment (width W): y=W2
- For the right segment (width W): y=W2
- Bottom segment: 0⋅L
- Top segment: W⋅L
- Left segment: W2⋅W
- Right segment: W2⋅W
Ycm=(0⋅L)+(W⋅L)+(W2⋅W)+(W2⋅W)L+2W
Ycm=WL+W2L+2W=W2
The coordinates of the center of mass from the corner of the rectangle are:
(L2,W2)
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-III
Explore 66 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-1(C.W.)
Explore 64 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
Knowledge Check
A uniform thin rod is bent in the form of closed loop ABCDEFA as shown in the figure. The y− coordinate of the centre of mass of the system is
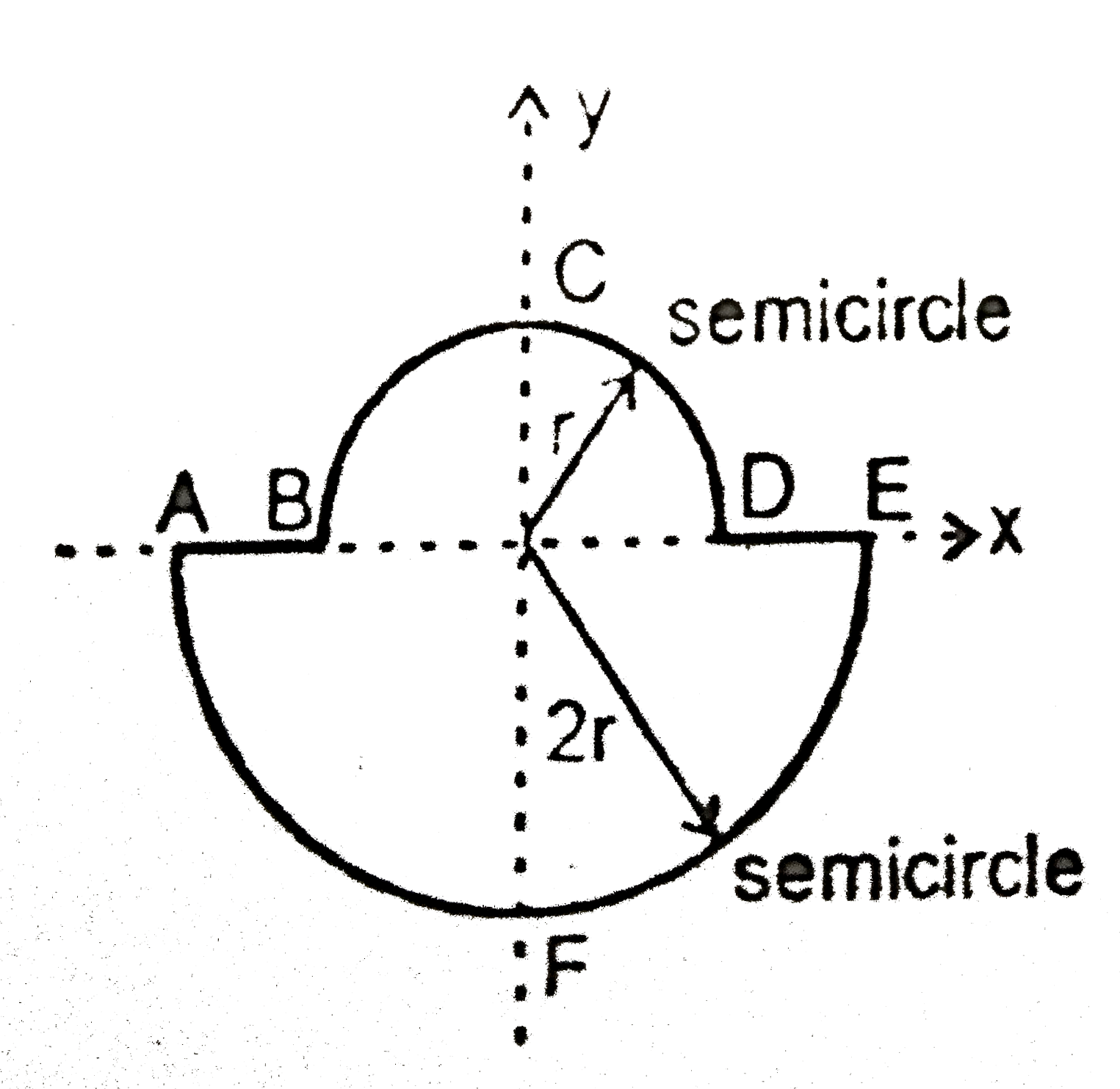 A2rπB−6r3π+2C−2rπDZero
A2rπB−6r3π+2C−2rπDZeroA uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-
 Al/2Bl√34Cl√38DNone of these
Al/2Bl√34Cl√38DNone of theseA uniform metre rod is bent into L shape with the bent arms at 90∘ to each other. The distance of the centre of mass from the bent point is
AL4√2mBL2√2mCL√2mDL8√2m
A wire in the form of a circle of radius 3.5 m is bent in the form of a rectangle, whose length and breadth are in the ratio of 6:5. What is the area of the rectangle?
View SolutionA wire in the form of a circle of radius 3.5 m is bent in the form of a rectangle, whose length and breadth are in the ratio of 6:5. What is the area of the rectangle?
View SolutionA wire is in the form of a square of side 18 m. It is bent in the form of a rectangle, whose length and breadth are in the ratio 3:1. The area of the rectangle is 81 m2 (b) 243 m2 (c) 144 m2 (d) 324 m2
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is

View SolutionA circular wire of diameter 77 cm is bent in the form of a rectangle whose length is 142% of its breadth. What is the area of the rectangle? (Take π=227)
View Solution