A circular hole of radius $r$ is made in a disk of radius $R$ and of uniform thickness at a distance $a$ from the centre of the disk. The distance of the new centre of mass from the original centre of mass is

A

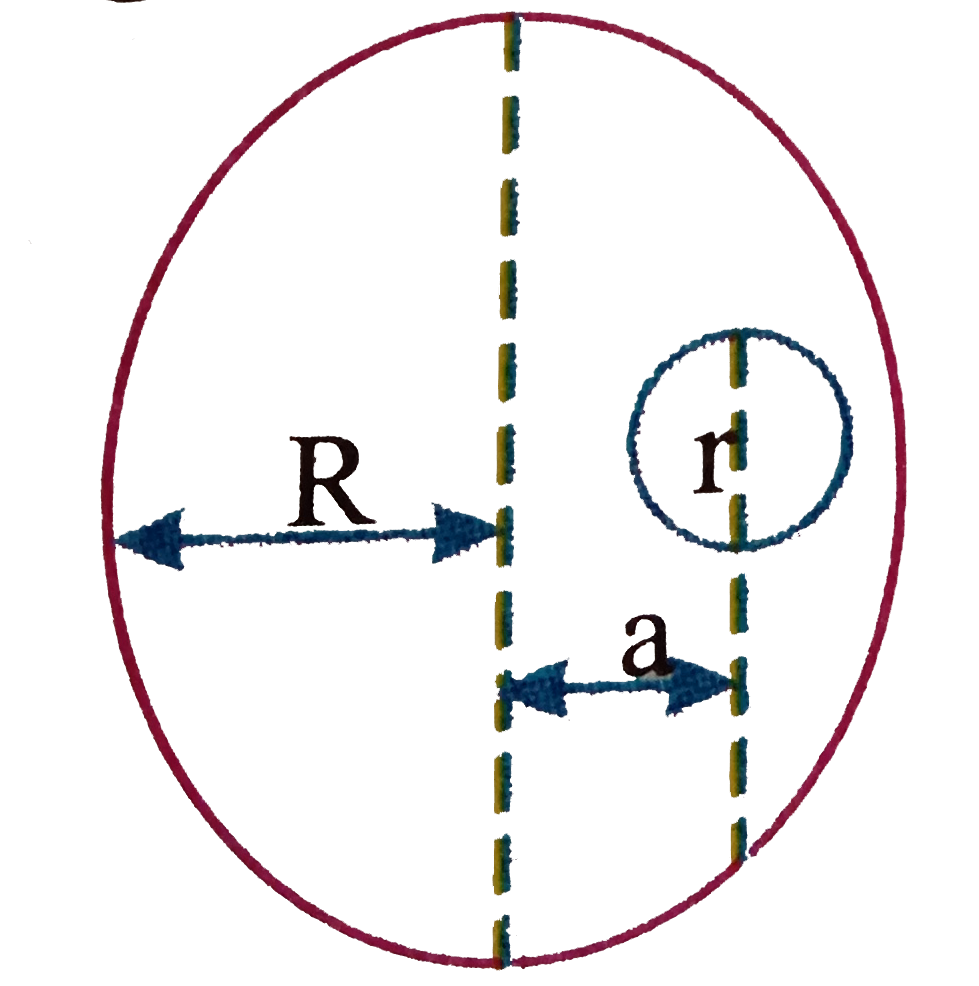
$\frac{a R^{2}}{R^{2} - r^{2}}$

B

$\frac{a r^{2}}{R^{2} - r^{2}}$

C

$\frac{a (R^{2} - r^{2})}{r^{2}}$

D

$\frac{a (R^{2} - r^{2})}{R^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$x = \frac{r^{2} a}{R^{2} - r^{2}}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A $\frac{3}{35} c m$
B $\frac{1}{35} c m$
C $\frac{3}{10} c m$
DNone of these
Question 2 - Select One
In the figure shown a hole of radius 2 cm is made in a semicircular disc of radius $6 π$ at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :

A4 cm
B8cm
C6 cm
D12 cm
Question 3 - Select One
A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance $x_{2}$ of the center of mass of the remaining part from the initial center of mass O is given by

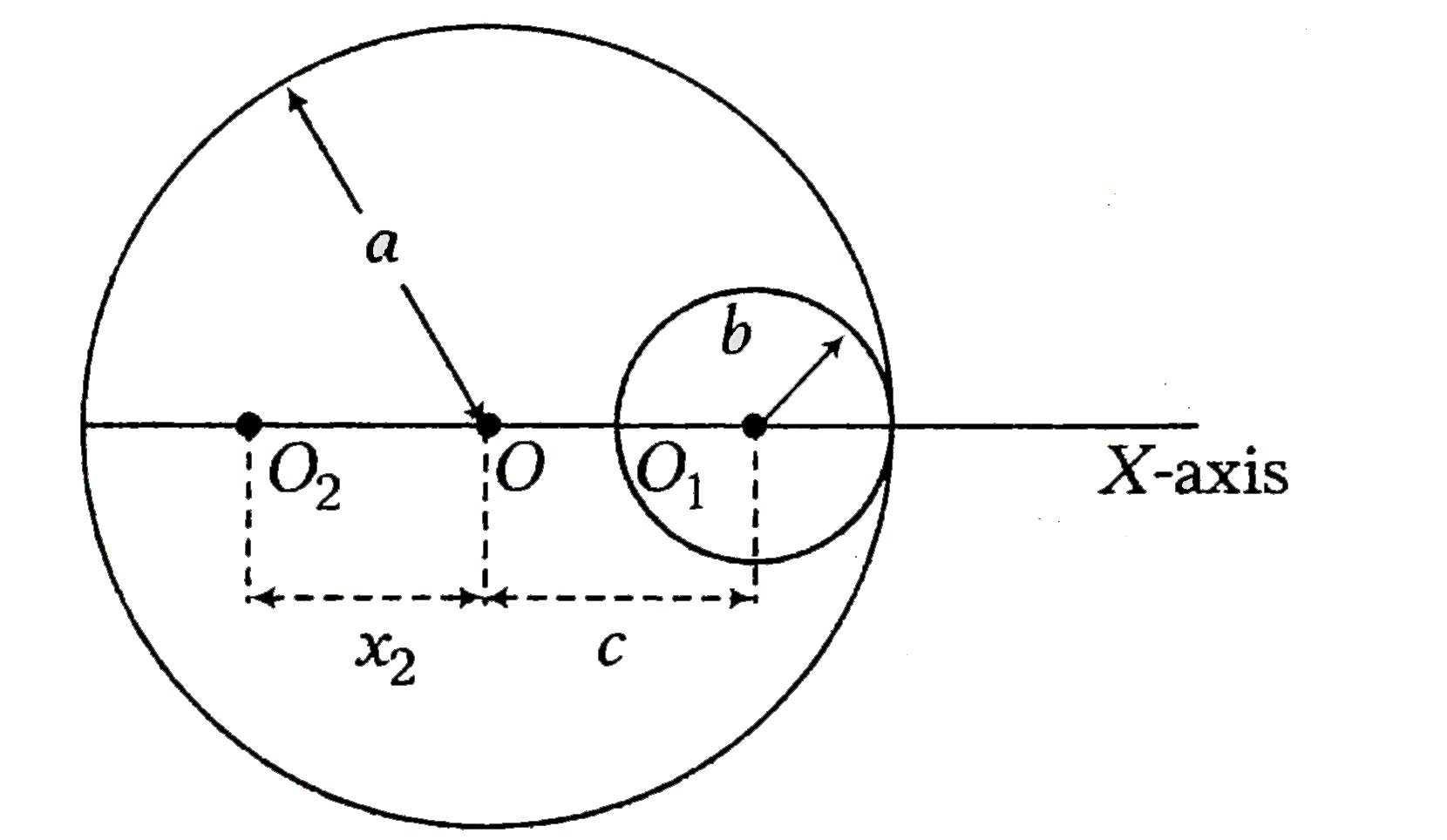A $\frac{π b^{2}}{(a^{2} - b^{2})}$
B $\frac{- c b^{2}}{(a^{2} - b^{2})}$
C $\frac{π c^{2}}{(a^{2} - b^{2})}$
D $\frac{π a^{2}}{(c^{2} - b^{2})}$

NARAYNA-SYSTEM OF PARTICLES-Level-II(C.W.)

Home
Ask Doubt
Profile