A roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
980N
1960N
2940N
3920N
The correct Answer is:D
To find the minimum horizontal force required to turn the roller onto the step, we can follow these steps:
Step 1: Understand the Problem
We have a roller of mass m=300kg and radius r=0.5m resting against a step of height h=0.2m. We need to determine the minimum horizontal force F needed to make the roller climb over the step.
Step 2: Identify the Forces Acting on the Roller
The forces acting on the roller include:
- The weight of the roller W=mg, where g≈9.81m/s2.
- The applied horizontal force F.
- The normal reaction force at the point of contact with the step.
Step 3: Calculate the Weight of the Roller
First, we calculate the weight of the roller:
W=mg=300kg×9.81m/s2=2943N
Step 4: Determine the Geometry of the Situation
When the roller begins to climb the step, the center of the roller will be lifted. The vertical distance from the center of the roller to the top of the step is:
Vertical distance=r−h=0.5m−0.2m=0.3m
Step 5: Set Up the Moment Equation
To find the minimum force F, we can set up the moment about the edge of the step. The moment due to the weight of the roller about the edge of the step must equal the moment due to the applied force F.
The distance from the edge of the step to the center of the roller is:
d=√r2−h2=√(0.5)2−(0.2)2=√0.25−0.04=√0.21≈0.458m
The moment due to the weight of the roller about the edge of the step is:
Moment due to weight=W⋅d=2943N⋅0.458m
The moment due to the applied force F is:
Moment due to force=F⋅h=F⋅0.2m
Step 6: Set the Moments Equal
Setting the moments equal gives us:
2943⋅0.458=F⋅0.2
Step 7: Solve for the Force F
Now, we can solve for F:
F=2943⋅0.4580.2≈1341.8340.2≈6709.17N
Final Answer
The minimum horizontal force required to turn the roller onto the step is approximately 6709.17N.
---
We have a roller of mass m=300kg and radius r=0.5m resting against a step of height h=0.2m. We need to determine the minimum horizontal force F needed to make the roller climb over the step.
The forces acting on the roller include:
- The weight of the roller W=mg, where g≈9.81m/s2.
- The applied horizontal force F.
- The normal reaction force at the point of contact with the step.
First, we calculate the weight of the roller:
W=mg=300kg×9.81m/s2=2943N
When the roller begins to climb the step, the center of the roller will be lifted. The vertical distance from the center of the roller to the top of the step is:
Vertical distance=r−h=0.5m−0.2m=0.3m
To find the minimum force F, we can set up the moment about the edge of the step. The moment due to the weight of the roller about the edge of the step must equal the moment due to the applied force F.
d=√r2−h2=√(0.5)2−(0.2)2=√0.25−0.04=√0.21≈0.458m
Moment due to weight=W⋅d=2943N⋅0.458m
Moment due to force=F⋅h=F⋅0.2m
Setting the moments equal gives us:
2943⋅0.458=F⋅0.2
Now, we can solve for F:
F=2943⋅0.4580.2≈1341.8340.2≈6709.17N
The minimum horizontal force required to turn the roller onto the step is approximately 6709.17N.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-III
Explore 66 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-1(C.W.)
Explore 64 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
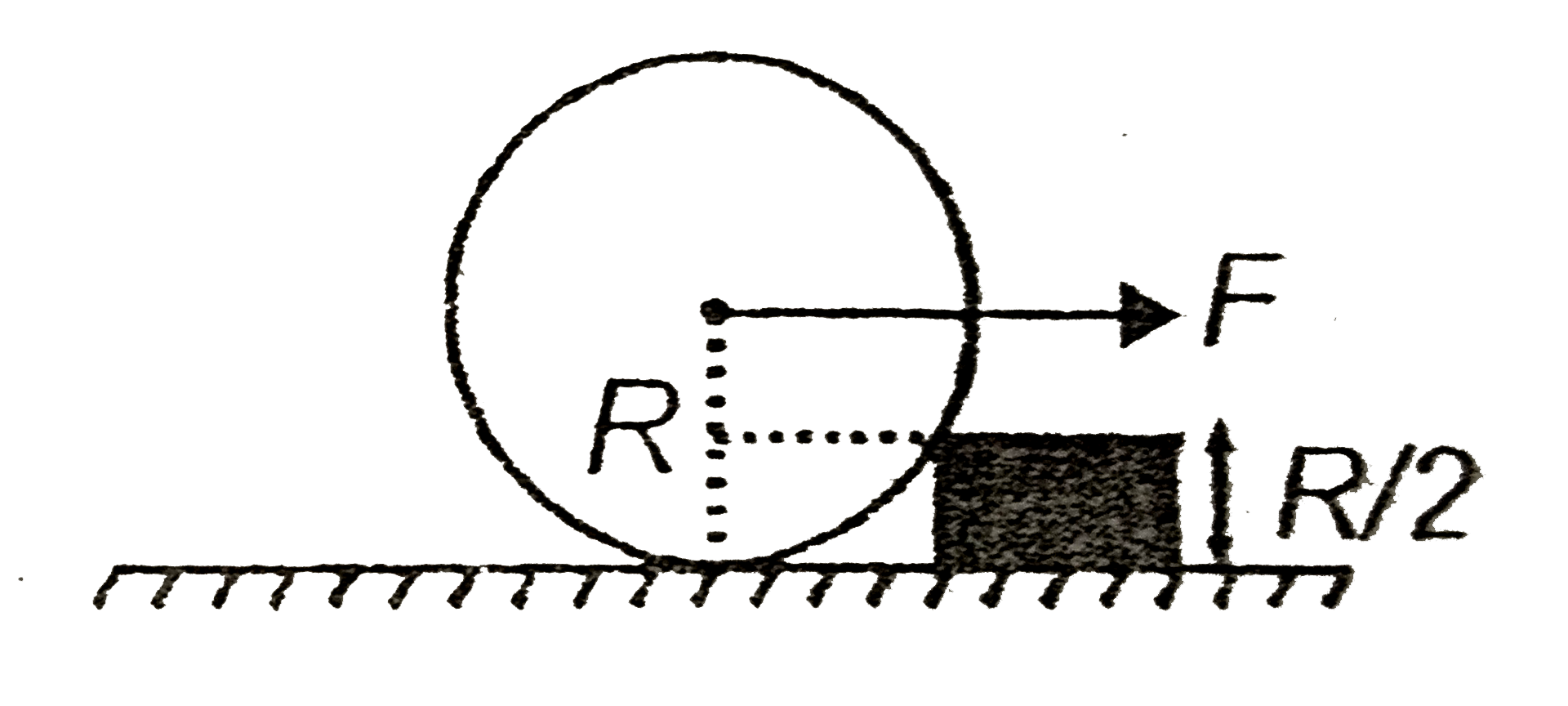
The minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
View SolutionA solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
View Solution
Knowledge Check
A wheel of radius r and mass m stands in front of a step of height h. The least horizontal force which should be applied to the axle of the wheel to allow it to raise onto the step is
 Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghr
Amgh(2r−h)r−hBmgh(r−h)Cmg(√h(2r−h))r−hDmghrA metallic cube of side length 1.5m and of mass 3.2 metric ton is on horizontal rough sloor. The minimum horizontal force that should be applied on the cube at a height 1.2m from that floor to turn the cube about its lower edge is
A1.96×103NB4.9×103NC1.96×104ND4.9×104NA vertical disc of mass 5kg and radius 50cm rests against a steo of height 25cm as shown in figure. What minimum horizontal force applied perpendicular to the axle will make the disc to climb the step ? Take g=10m/s2.
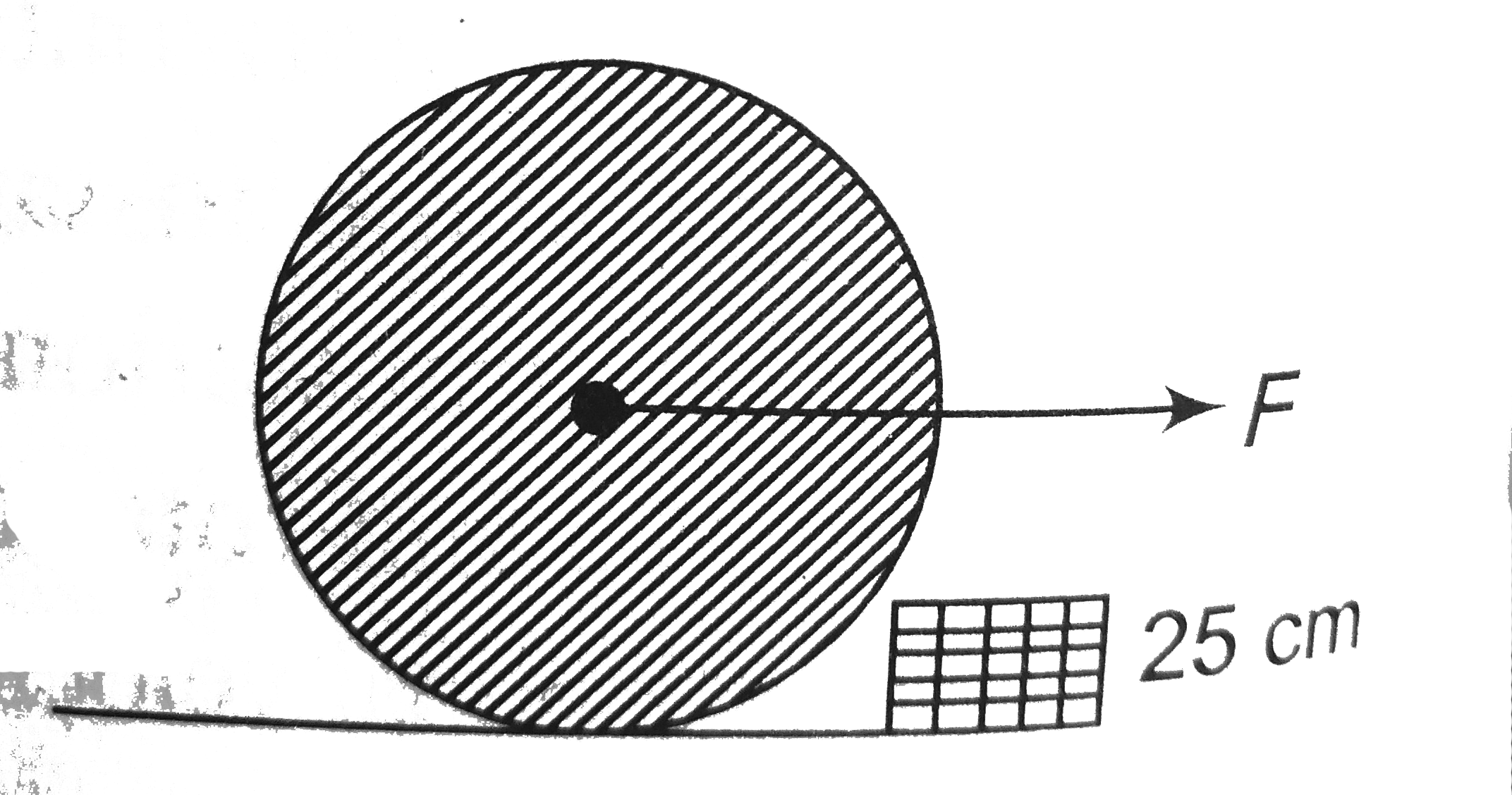 .A50 NB50√3NC25NDnone of these
.A50 NB50√3NC25NDnone of these
A solid cylindrical roller of mass M and radius R is rolled on a rough horizontal surface by applying a horizontal force F at the top most point. The frictional force between the roller and the surface, is
View SolutionA heavy wheel of radius 20cm and weight 10kg is to be dragged over a step of height 10cm, by a horizontal force F applied at the centre of the wheel. The minimum value of F is
View SolutionA staircase contains four steps each 10cm high and 20cm wide. The minimum horizontal velocity of a ball rolling off the uppermost plane so as to hit directly the lowest plane is
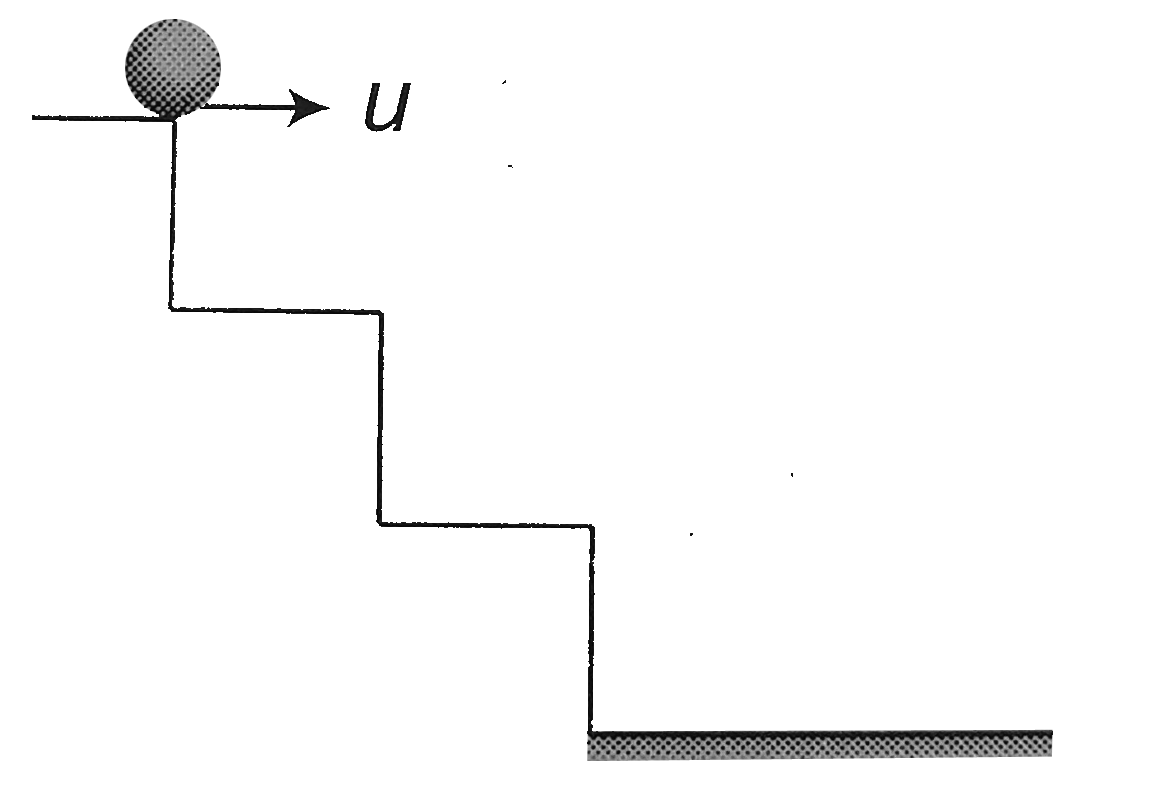
View SolutionA disc of radius 2 m and mass 100kg rolls on a horizontal floor, its centre of mass has speed of 20cm/s. How much work is needed to stop it ?
View SolutionA heavy and a light cylindrical rollers of diameter D and d respectively rest on a horizontal plane as shown. The larger roller has a string wound around it to which a horizontal force 'P' can be applied as shown. Assuming 'mu' (coefficient of friction) is same at all surfaces of contact, find the critical value of 'mu' such that larger roller can be just pulled over smaller one.

View Solution

