A metal rod of uniform thickness and of length is suspended at its division with help of a string. The rod remains horizontally straight when a block of mass is suspended to the rod at its division. The mass of rod is
The correct Answer is:C
To solve the problem, we will analyze the forces and torques acting on the metal rod when it is in equilibrium. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a metal rod of length 1 meter suspended at the 25 cm mark. A block of mass 2 kg is hanging from the 10 cm mark on the rod. We need to find the mass of the rod.
Step 2: Identify Forces Acting on the Rod
1. The weight of the rod acts downwards at its center of mass, which is at the 50 cm mark (since the rod is uniform).
2. The weight of the block (2 kg) acts downwards at the 10 cm mark.
3. The tension in the string acts upwards at the 25 cm mark.
Step 3: Set Up the Torque Equilibrium Equation
For the rod to be in rotational equilibrium, the sum of the torques about the point of suspension (25 cm mark) must be zero.
- Torque due to the weight of the rod (mass M):
- Distance from the 25 cm mark to the center of the rod (50 cm) = 50 cm - 25 cm = 25 cm
- Torque = Weight of rod (Mg) × Distance = Mg × 0.25 m
- Torque due to the weight of the block (2 kg):
- Distance from the 25 cm mark to the block (10 cm) = 25 cm - 10 cm = 15 cm
- Torque = Weight of block (2g) × Distance = 2g × 0.15 m
Step 4: Write the Torque Balance Equation
Setting the clockwise torque equal to the counterclockwise torque:
Mg×0.25=2g×0.15
Step 5: Simplify the Equation
We can cancel out g from both sides (assuming g≠0):
M×0.25=2×0.15
Step 6: Calculate the Mass of the Rod
Now, solve for M:
M×0.25=0.30
M=0.300.25=1.2 kg
Conclusion
The mass of the rod is 1.2 kg.
---
We have a metal rod of length 1 meter suspended at the 25 cm mark. A block of mass 2 kg is hanging from the 10 cm mark on the rod. We need to find the mass of the rod.
1. The weight of the rod acts downwards at its center of mass, which is at the 50 cm mark (since the rod is uniform).
2. The weight of the block (2 kg) acts downwards at the 10 cm mark.
3. The tension in the string acts upwards at the 25 cm mark.
For the rod to be in rotational equilibrium, the sum of the torques about the point of suspension (25 cm mark) must be zero.
- Distance from the 25 cm mark to the center of the rod (50 cm) = 50 cm - 25 cm = 25 cm
- Torque = Weight of rod (Mg) × Distance = Mg × 0.25 m
- Distance from the 25 cm mark to the block (10 cm) = 25 cm - 10 cm = 15 cm
- Torque = Weight of block (2g) × Distance = 2g × 0.15 m
Setting the clockwise torque equal to the counterclockwise torque:
We can cancel out g from both sides (assuming g≠0):
Now, solve for M:
The mass of the rod is 1.2 kg.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-III
Explore 66 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-1(C.W.)
Explore 64 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps (g=10m/s2).

View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gA uniform rod of mass m and length L is suspended with two massless strings as shown in the figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1T2 is:
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3A uniform rod of mass m and length L is suspended with two massless strings as shown in figure. If the rod is at rest in a horizontal position the ratio of tension in the two strings T1/T2 is
 A1:1B1:2C2:1D4:3
A1:1B1:2C2:1D4:3
A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionA uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionA uniform rod of mass and length l is suspended by two strings at its ends shown. When one of the strings is cut, the rod starts falling with an initial angular acceleration.
View SolutionA uniform metal rod of length 1m is bent at 90∘, so as to form two arms of equal length. The centre of mass of this bent rod is
View SolutionA particle of mass m is attached to an end of a uniform rod of mass M = 2m and length l1 which is suspended through its mid point by an inextensible string as shown initially the rod is in horizontal position and at rest. The system is released from this position Just after the release
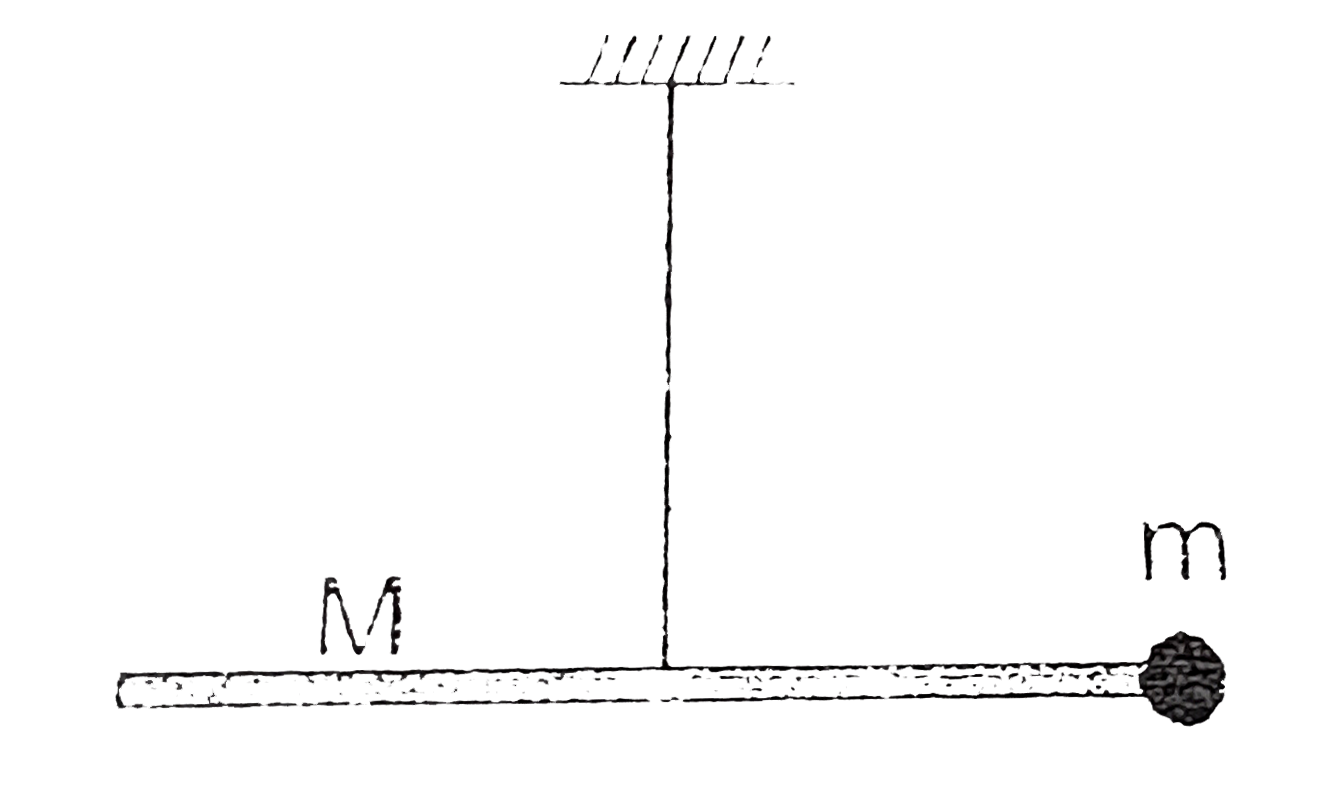
View Solution

