Question

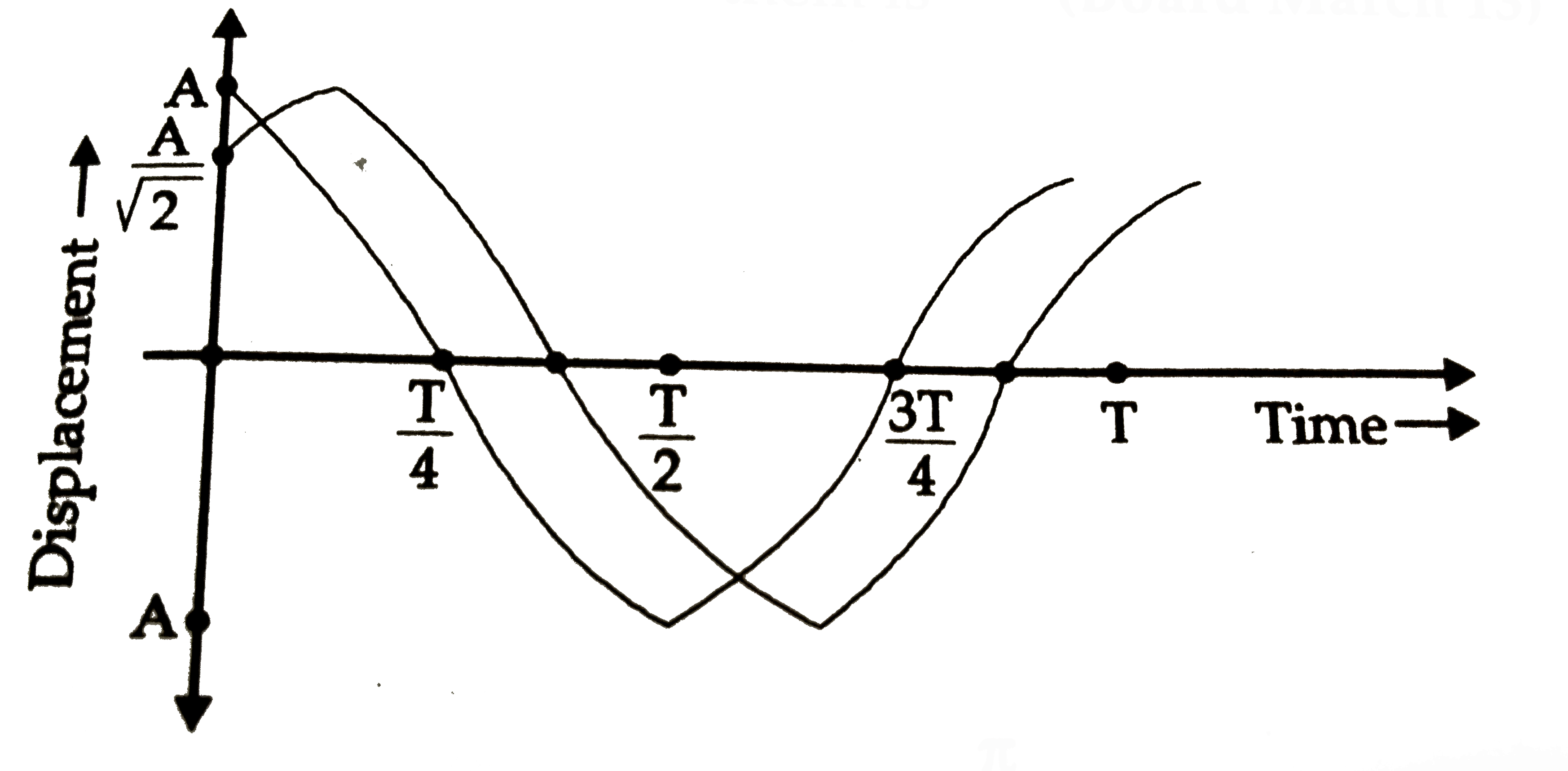
Two particles A and B execute simple harmonic motions of period T and $5T/4$. They start from mean position. The phase difference between them when the particle A complete an oscillation will be

Options

A. `pi//2`
B. `0`
C. `2pi//5`
D. `pi//4`

Answer

C

Explanation

To find the phase difference between two particles A and B executing simple harmonic motion (SHM) when particle A completes one oscillation, we can follow these steps:

Step 1: Identify the periods of the two particles
- Particle A has a period \( T_A = T \).
- Particle B has a period \( T_B = \frac{5T}{4} \).

Step 2: Calculate the angular frequencies (ω) of both particles
- The angular frequency \( \omega \) is given by the formula:
\( \omega = \frac{2\pi}{T} \)
- For particle A:
\( \omega_A = \frac{2\pi}{T} \)
- For particle B:
\( \omega_B = \frac{2\pi}{T_B} = \frac{2\pi}{\frac{5T}{4}} = \frac{8\pi}{5T} \)

Step 3: Determine the phase of each particle at time \( t \)
- Since both particles start from the mean position, their phases at any time \( t \) can be expressed as:
\( \phi_A = \omega_A t = \frac{2\pi}{T} \cdot t \)
\( \phi_B = \omega_B t = \frac{8\pi}{5T} \cdot t \)

Step 4: Calculate the phase difference (Δφ) at time \( t \)
- The phase difference between the two particles at any time \( t \) is given by:
\( \Delta \phi = \phi_A - \phi_B \)
- Substituting the expressions for \( \phi_A \) and \( \phi_B \):
\( \Delta \phi = \left(\frac{2\pi}{T} t\right) - \left(\frac{8\pi}{5T} t\right) \)
- Factoring out \( t \):
\( \Delta \phi = t \left(\frac{2\pi}{T} - \frac{8\pi}{5T}\right) \)
- Simplifying the expression:
\( \Delta \phi = t \left(\frac{2\pi \cdot 5 - 8\pi}{5T}\right) = t \left(\frac{10\pi - 8\pi}{5T}\right) = t \left(\frac{2\pi}{5T}\right) \)

Step 5: Evaluate the phase difference when particle A completes one oscillation
- Particle A completes one oscillation at \( t = T \):
\( \Delta \phi = T \left(\frac{2\pi}{5T}\right) = \frac{2\pi}{5} \)

Conclusion
The phase difference between particles A and B when particle A completes one oscillation is:
\( \Delta \phi = \frac{2\pi}{5} \)