The amplitude and maximum velocity will be respectively X=3sin2t+4cos2tThe amplitude and maximum velocity will be respectively
5,10
3,2
4,2
3,4
The correct Answer is:A
x=3sin2t+4cos2t
=5[35sin2t+45cos2t]
=5[cosαsin2t+sinαcos2t]
x=5sin(2t+α)
v=dxdt=5×2cos(2t+α)
=10cos(2t+α)
Amplitude A=5, vmax=10
Alternatively:
x=3sin2t+4cos2t
=3sin2t+4sin(2t+π2)
x=Asin(2t+α)
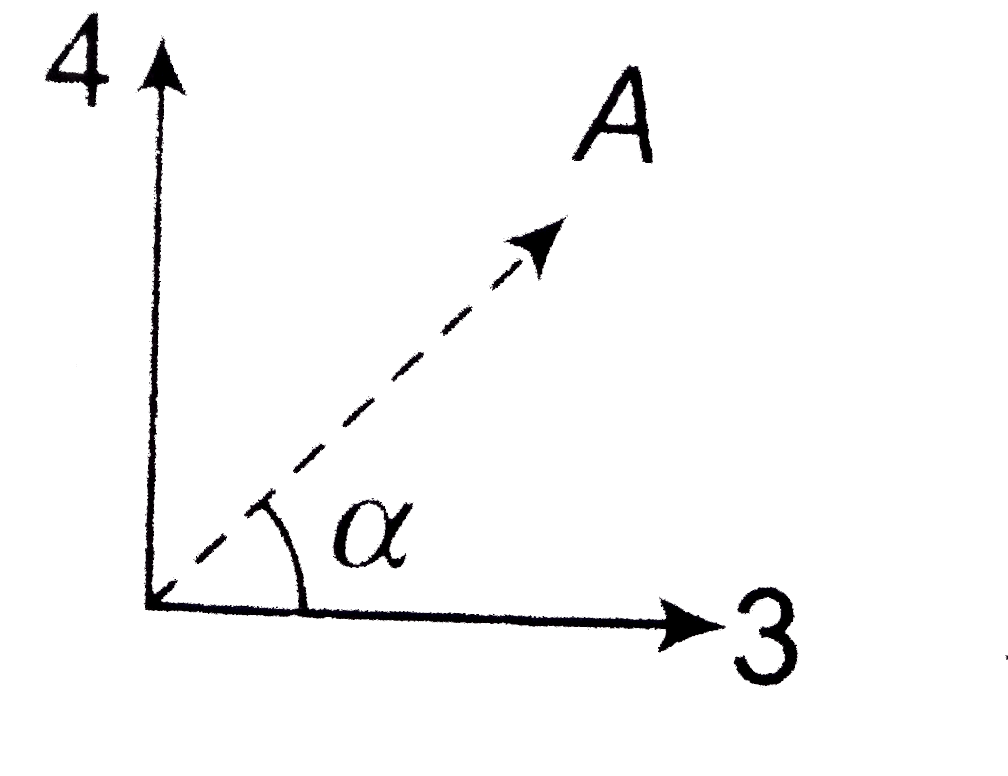
A=√32+42=5
tanα=43
x=5sin(2t+α)
v=dxdt=5×2cos(2t+α)
=10cos(2t+α)
v is maximum when cos(2t+α)=1
vmax=10
Topper's Solved these Questions
Similar Questions
If the maximum and minimum value of sinsinx is a and b respectively and the maximum and minimum value of coscosx is c and d respectively then a2+b2+c2+d2: (A) 1+a2 (B) 2+a2 (C) 3+a2 (D) 4+a2
View SolutionA particle is executing S.H.M. with amplitude 'A' and maximum velocity Vm. The displacement at which its velocity is half of the maximum velocity is
View Solution
Knowledge Check
If S=9t−3t3, then maximum velocity is
A0B−9 units / secC9 units/ SecD10 units /secA SHO has amplitude A and time period T. The maximum velocity will be
A4ATB2ATC2π√A/TD2πA/TFor a particle in SHM the amplitude and maximum velocity are A and V respectively. Then its maximum acceleration is
AV22ABV2ACV2ADVA
In a plane progressive wave given by y=25cos(2πt−πx), the amplitude and frequency are respectively
View SolutionIf S=16+64t−t3, then maximum velocity is
View SolutionThe velocity-time graph of a particle executing SHM is as shown in the figure. The amplitude and maximum acceleration of the particle respectively are
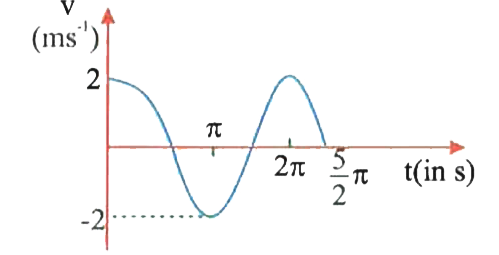
View SolutionEquation of displacement of a harmonic oscillator is x=15sin20πt, amplitude and angular velocity are respectively
View SolutionThe displacement ξ in centimetres of a particle is ξ=3sin314t+4cos314t. Amplitude and initial phase are
View Solution
