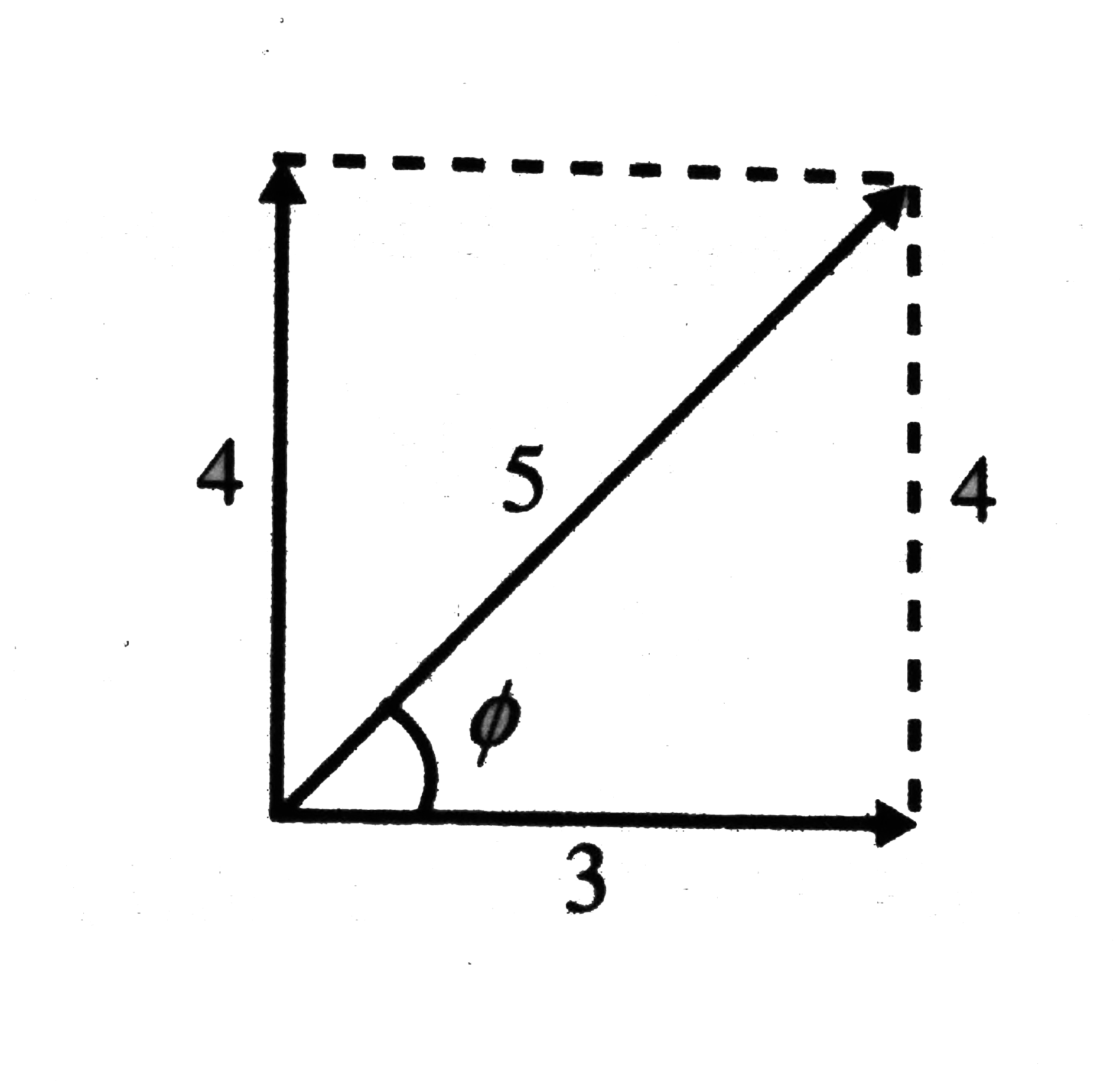
The displacement $ξ$ in centimetres of a particle is $ξ = 3 sin 314 t + 4 cos 314 t$ . Amplitude and initial phase are

A

$5 c m, {tan}^{- 1} (\frac{4}{3})$

B

$3 c m, \frac{{tan}^{- 1} (3)}{4}$

C

$4 c m, \frac{{tan}^{- 1} (4)}{9}$

D

$4 c m, 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$a = \sqrt{3^{2} + 4^{2}} = \sqrt{9 + 16} = \sqrt{25} = 5 c m$
$tan ϕ = \frac{4}{3} or ϕ = {tan}^{- 1} (\frac{4}{3})$

|

Updated on:21/07/2023

Class 11 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The displacement of a particle performing S.H.M. is x = 3 sin (314 t) + 4 cos (314 t). Then the initial phase angle is,
A ${tan}^{- 1} (7)$
B ${tan}^{- 1} (4)$
C ${tan}^{- 1} (3)$
D ${tan}^{- 1} (4 / 3)$
Question 2 - Select One
The displacement of a particle is given by $x = 3 sin (5 π t) + 4 cos (5 π t)$ . The amplitude of particle is
A $3$
B $4$
C $5$
D $7$
Question 3 - Select One
The displacement of a particle in $S H M$ is $x = 3 sin (20 π t) + 4 cos (20 π t) c m$ . Its amplitude of oscillation is
A $3 c m$
B $4 c m$
C $5 c m$
D $25 c m$

CENGAGE PHYSICS-SUPERPOSITION AND STANDING WAVES-Single Correct

Home
Ask Doubt
Profile