A sound wave of wavelength 0.40m enters the tube at S. The smallest radius r of the circular segment to hear minimum at detector D must be

1.75m
0.175m
0.93m
9.3m
The correct Answer is:B
Path difference =(πr−2r)
=(2n−1)λ/2 for minima
Given λ=0.40m , for smallest radius n=1(3.14−2)r=λ/2
r=λ2×1.14=0.402×1.14=0.175m
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Multiple
Explore 26 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Assertion - Reasoning
Explore 6 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICSChapter:SUPERPOSITION AND STANDING WAVESExercise:Subjective
Explore 24 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
Two sound waves of wavelength 1 m and 1.02 m produces 16 beats in 2 s in a medium then the velocity of the sound in that medium is
View SolutionTwo sources of sound, S1andS2 , emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S_1S_2 and at a distance of 20.0 cm from P it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through wffich the detector should be shifted to detect a minimum of sound.
View Solution
Knowledge Check
A sound wave of wavelength 32 cm enters the tube at S as shown in the figure. Then the smallest radius r so that a minimum of sound is heard at detector D is
 A7cmB14cmC21cmD28cm
A7cmB14cmC21cmD28cmTwo sound waves of wavelength 10 m and 10.1 m produces 0.33 beats/s. Then the velocity of sound is
A330 m/sB320 m/sC310 m/sD333.3 m/sTwo sound waves of wavelength 1m and 1.01m in a gas produce 10 beats in 3s. The velocity of sound in the gas is
A330m/sB337m/sC360m/sD300m/s
Figure shows two isotropic point sources of sound, S1 and S2 The sources emit waves in phase at wavelength 0.50 m, they are separated by D = 2.20 m. If we move a sound detector along a large circle centered at the midpoint between the sources, at how many points do waves arrive at the detector (a) exactly in phase and (b) exactly out of phase?

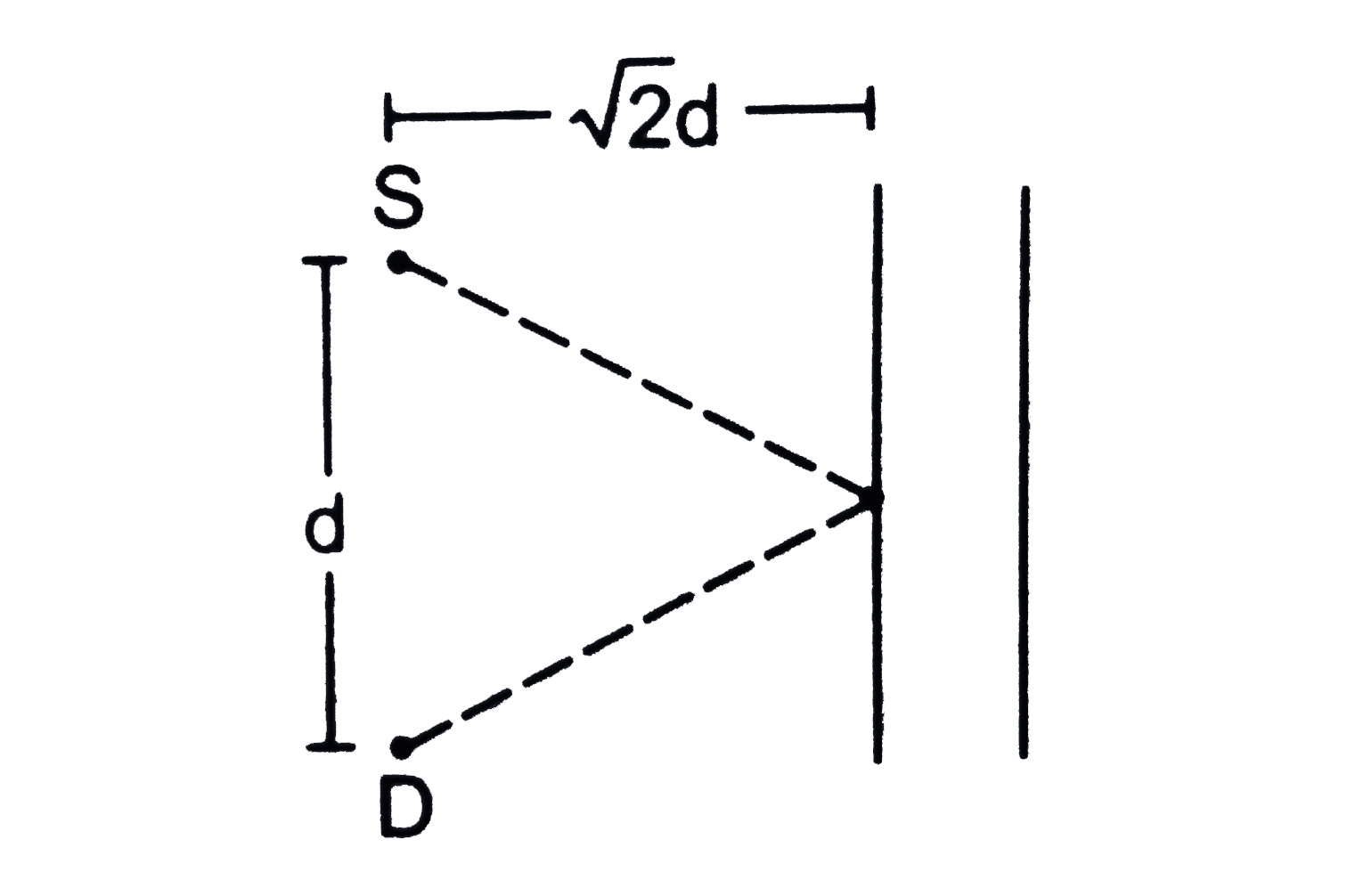
View SolutionA source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance √2d from the source and the detector as shown in figure. The source emits a wave of wavelength =d2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave ?
View SolutionTwo waves of wavelength 40 cm and 42 cm produce 15 beats s−1. The velocity of sound will be
View SolutionA sound wave of wavelength 90cm in glass is reflected into air. If the speed of sound in glass is 5400m/s, the wavelength of wave in air (speed of sound in air =330m/s) is :
View SolutionA sound wave of wavelength 90 cm in glass is refracted into air. If the velocity of sound in glass is 5400 m/s, then wavelength of the wave in air is
View Solution

