Two particles execute SHM of the same time period along the same straight lines. They cross each other at the mean position while going in opposite directions. Their phase difference is

A

$\frac{π}{2}$

B

$π$

C

$\frac{3 π}{2}$

D

$2 π$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:B

To solve the problem of finding the phase difference between two particles executing simple harmonic motion (SHM) that cross each other at the mean position while moving in opposite directions, we can follow these steps:
Step 1: Understand the SHM Characteristics
Both particles have the same time period and are moving along the same straight line. In SHM, the position of a particle can be described by the equation:
$x (t) = A sin (ω t + ϕ)$
where $A$ is the amplitude, $ω$ is the angular frequency, $t$ is time, and $ϕ$ is the phase constant.
Step 2: Analyze the Crossing at the Mean Position
The mean position in SHM corresponds to the position $x = 0$ . When the particles cross each other at this position, they are moving in opposite directions. This indicates that one particle is moving towards the mean position while the other is moving away from it.
Step 3: Determine the Phase of Each Particle
1. Particle 1: Let’s assume Particle 1 is at the mean position and moving upwards (towards the positive amplitude). The phase angle for this position can be represented as:
$ϕ_{1} = \frac{π}{2} (90 degrees)$
This is because at $ϕ = \frac{π}{2}$ , the sine function reaches its maximum value.
2. Particle 2: Since Particle 2 is also at the mean position but moving downwards (towards the negative amplitude), its phase angle can be represented as:
$ϕ_{2} = \frac{3 π}{2} (270 degrees)$
At this phase, the sine function is at zero but moving in the negative direction.
Step 4: Calculate the Phase Difference
The phase difference $Δ ϕ$ between the two particles can be calculated as:
$Δ ϕ = ϕ_{2} - ϕ_{1} = \frac{3 π}{2} - \frac{π}{2} = π$
This indicates that the phase difference is $π$ radians, or 180 degrees.
Conclusion
The phase difference between the two particles executing SHM and crossing each other at the mean position while moving in opposite directions is:
$Δ ϕ = π radians (or 180 degrees)$

Updated on:7/8/2024

|

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particles executes S.H.M. of the same amplitude and frequency along the same straight line. They pass one another when going in opposite directions, each time their displacement is root three by two times amplitude. The phase difference between them is
A $\frac{2 π}{3}$ rad
B $\frac{π}{2}$ rad
C $\frac{π}{6}$ rad
D $\frac{π}{3}$ rad
The phase difference between two particle executing $S H M$ of the same amplitude and frequency along same straight line while pessing one another when going in apposition direction with equal displacement from then respectively straing about is is $2 π / 3$ if the prass if one particle is $π / 6$ find the displecement at this instant amplitude is $A$
A $A / 3$
B $2 A / 3$
C $3 A / 4$
D $A / 2$
A: The phase difference between the two particles shown below is $π$ . (Assuming both particles have same time periods and same amplitudes).

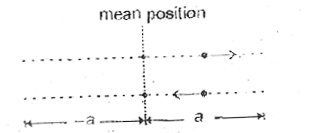
R: If the particles cross each other while they move in the opposite direction, they have a phase difference of $π$ radian.
AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1)
BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2)
CIf Assertion is true statement but Reason is false then mark (3)
DIf both Assertion and Reason are false statements, then mark (4)

CP SINGH-SIMPLE HARMONIC MOTION-Exercises

Home
Ask Doubt
Profile