A bullet is moving horizontally with certain velocity. It pierces two paper discs rotating coaxially with angular speed ω separated by a distance l. IF the hole made by bullet on second disc is shifted by an angle θ with respect to the first, find velocity of bullet.
ωl
lθω
ωlθ
ωl(θ)2
The correct Answer is:C
Step by step video, text & image solution for A bullet is moving horizontally with certain velocity. It pierces two paper discs rotating coaxially with angular speed omega separated by a distance l. IF the hole made by bullet on second disc is shifted by an angle theta with respect to the first, find velocity of bullet. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - COMPETITIVE THINKING
102 Videos
- ATOMS, MOLECULES AND NUCLEI BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Evaluation test
19 Videos
- CURRENT ELECTRICITY BOOK - TARGET PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - Evaluation Test
6 Videos
Similar Questions
Two paper discs are mounted on a rotating vertical shaft. The shaft rotates with a constant angular speed ω and the separation between the discs is H. A bullet is fired vertically up so that it pierces through the two discs. It creates holes H1 and H2 in the lower and the upper discs. The angular separation between the two holes (measured with respect to the shaft axis) is θ. Find the speed (v) of the bullet. Assume that the speed of the bullet does not change while travelling through distance H and that the discs do not complete even one revolution in the interval the bullet pierces through them.
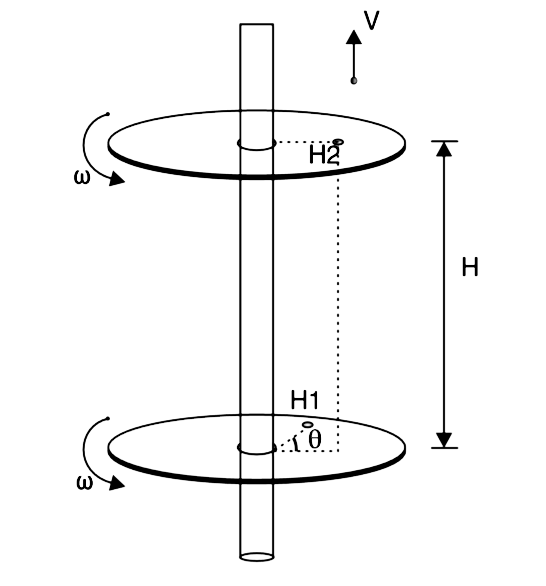
View SolutionA disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View Solution
Knowledge Check
A rough disc of mass m rotates freely with an angular velocity ω. If another rough disc of mass m2 and same radius but spinning in opposite sense with angular speed ω is kept on the first disc. Then:
Athe final angular speed of the dise is ω3Bthe net work does by friction is zeroCthe friction does a positive work on the lighter discDthe net work done by friction is −mR2ω23The figure shows a system consisting of (i) a ring the outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed ω and (ii) an inner disc of radius 2R rotating anti clockwise with angular speed ω/2. The ring and disc are separated. The point P on the inner disc is at a distance R from the origin, where OP makes an angle of 30∘ with the horizontal. Then with respect to the horizontal surface,
Athe point O has linear velocity 3RωˆiBthe point P has linear velocity 114Rωˆi+√34Rωˆk.Cthe point P has linear velocity 134Rωˆi−√34RωˆkDthe point P has linear velocity ((3−√34)Rωˆi+14Rωˆk.A horizontal turn table in the form of a disc of radius r carries a gun at G and rotates with angular velocity ω0 about a vertical axis passing through the centre O. The increase in angular velocity of the system if the gun fires a bullet of mass m with a tangential velocity v with respect to the gun is (moment of inertia of gun + table about O is I0
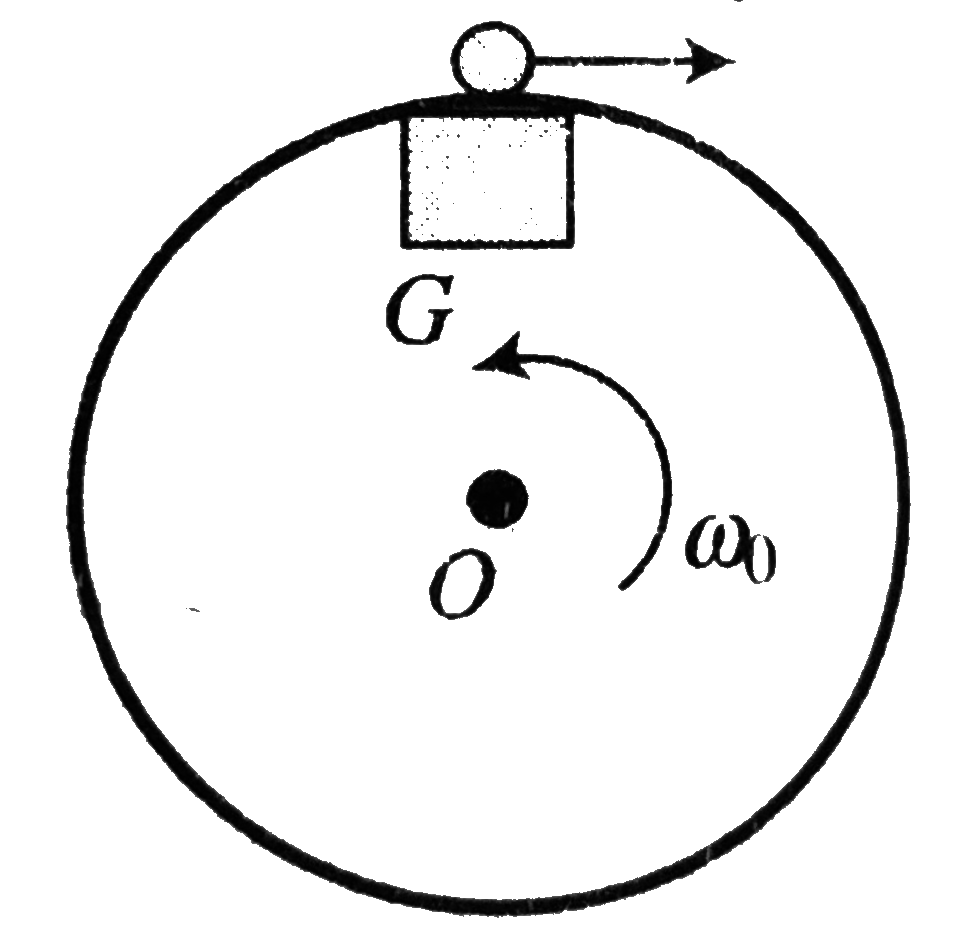 AmvrI0+mr2B2mvrI0Cv2rDmvr2I0
AmvrI0+mr2B2mvrI0Cv2rDmvr2I0
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA bullet of mass m collides inelastically at the periphery of a disc of mass M and radius R, with a speed v as shown. The disc rotates about a fixed horizontal axis. Find the angular velocity of the disc bullet system just after the impact.

View SolutionA rotating disc moves in the positive direction of x-axis as shown. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment the centre C of the disc was located at origin after which
a. it moved with constant acceleration a (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity ω. b. it moved with constant velocity v while the disc started rotating anticlockwise with a constant angular acceleration a (with initial angular velocity zero).

View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. another disc of the same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is 2ω/√5.
View SolutionIf two disc of moment of inertia l1 and l2 rotating about collinear axis passing through their centres of mass and perpendicular to their plane with angular speeds ω1 and ω2 respectively in opposite directions are made to rotate combinedly along same axis, then the magnitude of angular velocity of the system is
View Solution
