For a particle moving in a circle,
the resultant force on the particle must be towards the centre
the cross product of tangential acceleration and angular velocity will be zero
direction of angular acceleration and angular velocity must be same
the resultant force must be away from the centre
The correct Answer is:A
Step by step video, text & image solution for For a particle moving in a circle, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBook:TARGET PUBLICATIONChapter:CIRCULAR MOTIONExercise:COMPETITIVE THINKING
Explore 102 Videos
- ATOMS, MOLECULES AND NUCLEI Book:TARGET PUBLICATIONChapter:ATOMS, MOLECULES AND NUCLEI Exercise:Evaluation test
Explore 19 Videos
- CURRENT ELECTRICITY Book:TARGET PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:Evaluation Test
Explore 6 Videos
Similar Questions
The angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
View SolutionConsider a particle , moving in a circle with constant speed . P is a point outside the circle , in the same plane . Then , the angular momentum of the particle about the point P is
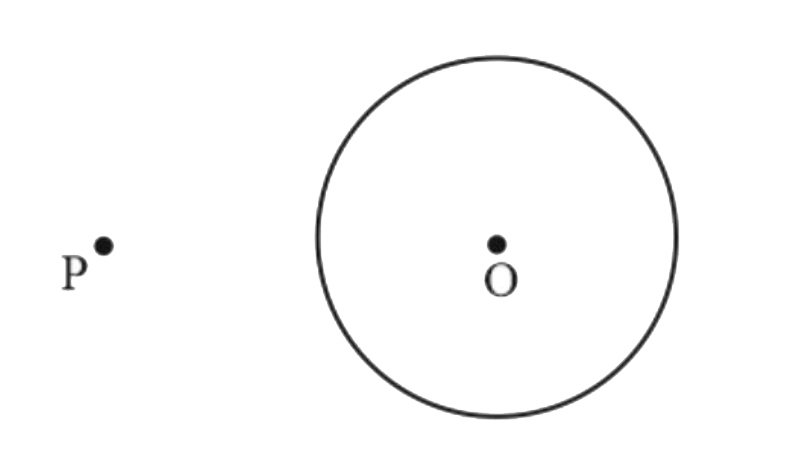
View Solution
Knowledge Check
The speed of a particle moving in a circle is increasing. The dot product of its acceleration and velocity is
AnegativeBzeroCpositiveDmay be positive or negativeFind the magnitude of the linear acceleration of a particle moving in a circle of radius 10 cm with uniform speed completing the circle in 4s.
A1.5π2B2.5π2C3.5π2D4.5π2The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed ω varries with time t is
A2asinωtB2asin(ωt2)C2acosωtD2acos(ωt2)
The speed (v) of a particle moving in a circle of radius R varies with distance s as v=ks where k is a positive constant.Calculate the total acceleration of the particle
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
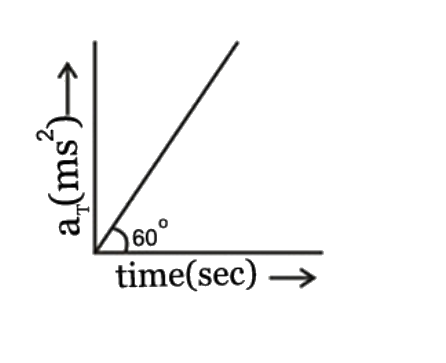
View SolutionCalculate the linear acceleration of a particle of a particle moving in a circle of radius 0.4 m at the instant when its angular velocity is 2 rad s−1 and its angular acceleration is 5 rad s−2.
View SolutionThe speed of a particle moving in a circle slows down at a rate of 3m/sec2. At some instant the magnitude of the total acceleration is 5msec2 and the particle's speed is 12 m/sec. The radius of circle will be :
View SolutionThe angular velocity of a particle moving in a circle of radius 50cm is increased in 5 min from 100 revolutions per minute to 400 revolutions per minute. Find the tangential acceleration of the particle.
View Solution
