A ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition.
53∘
37∘
45∘
47∘
The correct Answer is:A
Step by step video, text & image solution for A ball suspended by a thread swing in a vertical plane that its acceleration values in the lowest possition and the extreme postition are equal . Find the thread deffection angle in the extreme possition. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCULAR MOTIONBook:TARGET PUBLICATIONChapter:CIRCULAR MOTIONExercise:COMPETITIVE THINKING
Explore 102 Videos
- ATOMS, MOLECULES AND NUCLEI Book:TARGET PUBLICATIONChapter:ATOMS, MOLECULES AND NUCLEI Exercise:Evaluation test
Explore 19 Videos
- CURRENT ELECTRICITY Book:TARGET PUBLICATIONChapter:CURRENT ELECTRICITY Exercise:Evaluation Test
Explore 6 Videos
Similar Questions
(a) A ball, suspended by a thread, swings in a vertical plane so that the magnitudes of its acceleration in the extreme and the lowest positions are equal. Find the maximum deflection of the thread with respect to the vertical.
( b) The kinetic energy of a particle moving in a circle of radius R depens on the distance covered as T=as2 , where 'a' is a constant. Find the magnitude of the force acting on the particle as a function of s.
View SolutionA small bob suspended by a thread swings in a vertical plane so that angle made by thread in extreme positions with the vertical is θ=sin−1(45) What is the ratio of acceleration of bob in extreme position to its acceleration in lowest position?
View Solution
Knowledge Check
A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
Atan−1(2)Btan−1(√2)Ctan−1(12)D2tan−1(12)A ball suspended by a thread swings in a vertical plane so that its acceleration in the extreme position and lowest position are equal. The angle of thread deflection in the extreme position will be - 2
Atan−1(2)Btan−1(√2)Ctan−1(12)D2tan−1(12)A ball attached to one end of a stringj swings in a vertical plane such that its acceleration at point A (exterme posiuion) is eqal to its acceleration at point B (mean posirion), The angle θ is
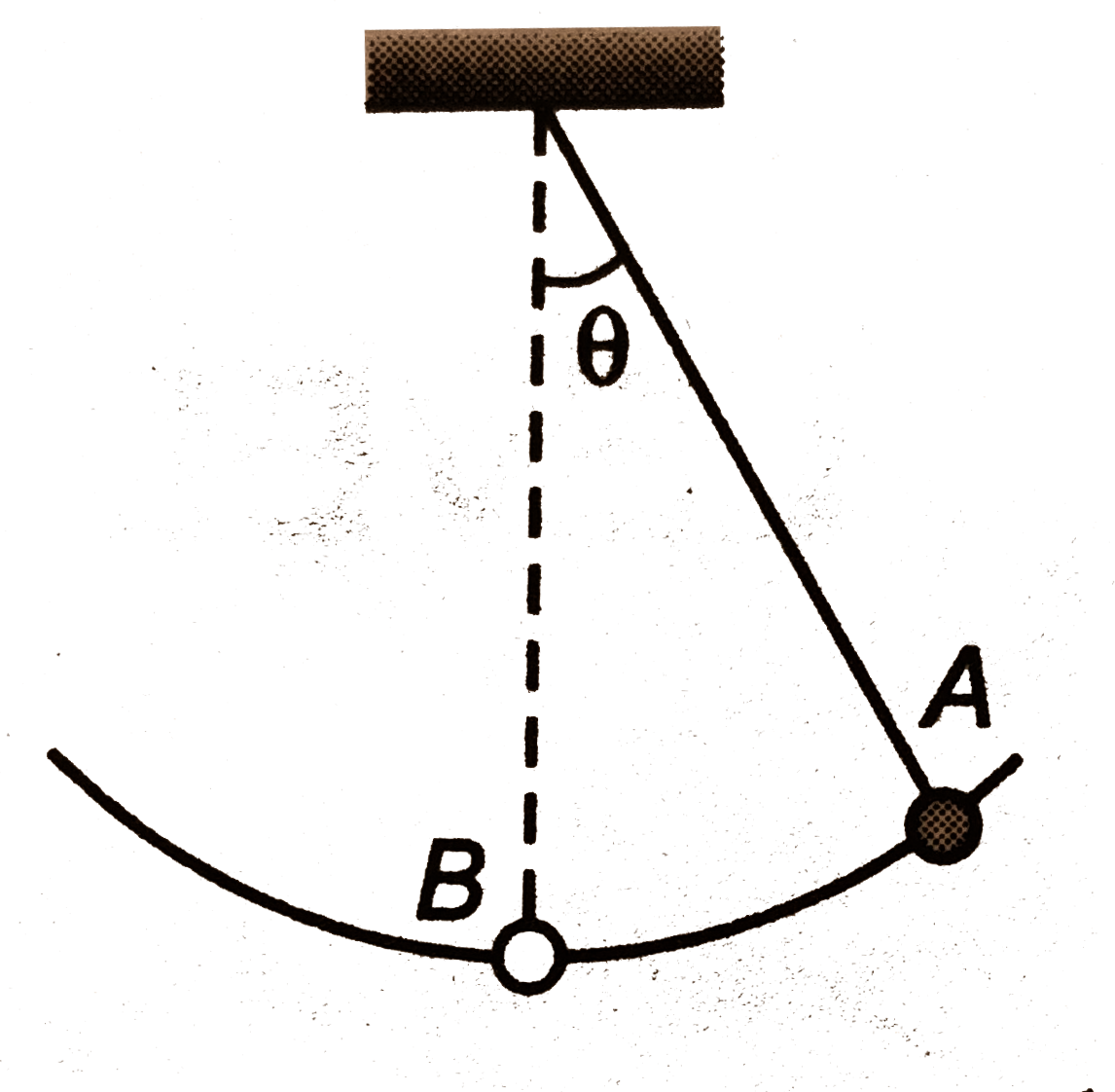 Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of these
Acos−1(25)Bcos−1(45)Ccos−1(35)DNone of these
A rod of mass m and length l suspended from a point swings in a vertica plane such that magnitude of acceleration of its C.M. at extreme points is same as that at the mean point then :
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is (a)the thread is displacement through a small angle away from the vertical and (b) the ball is released. Find the period of oscillation of pendulum. Consider both cases
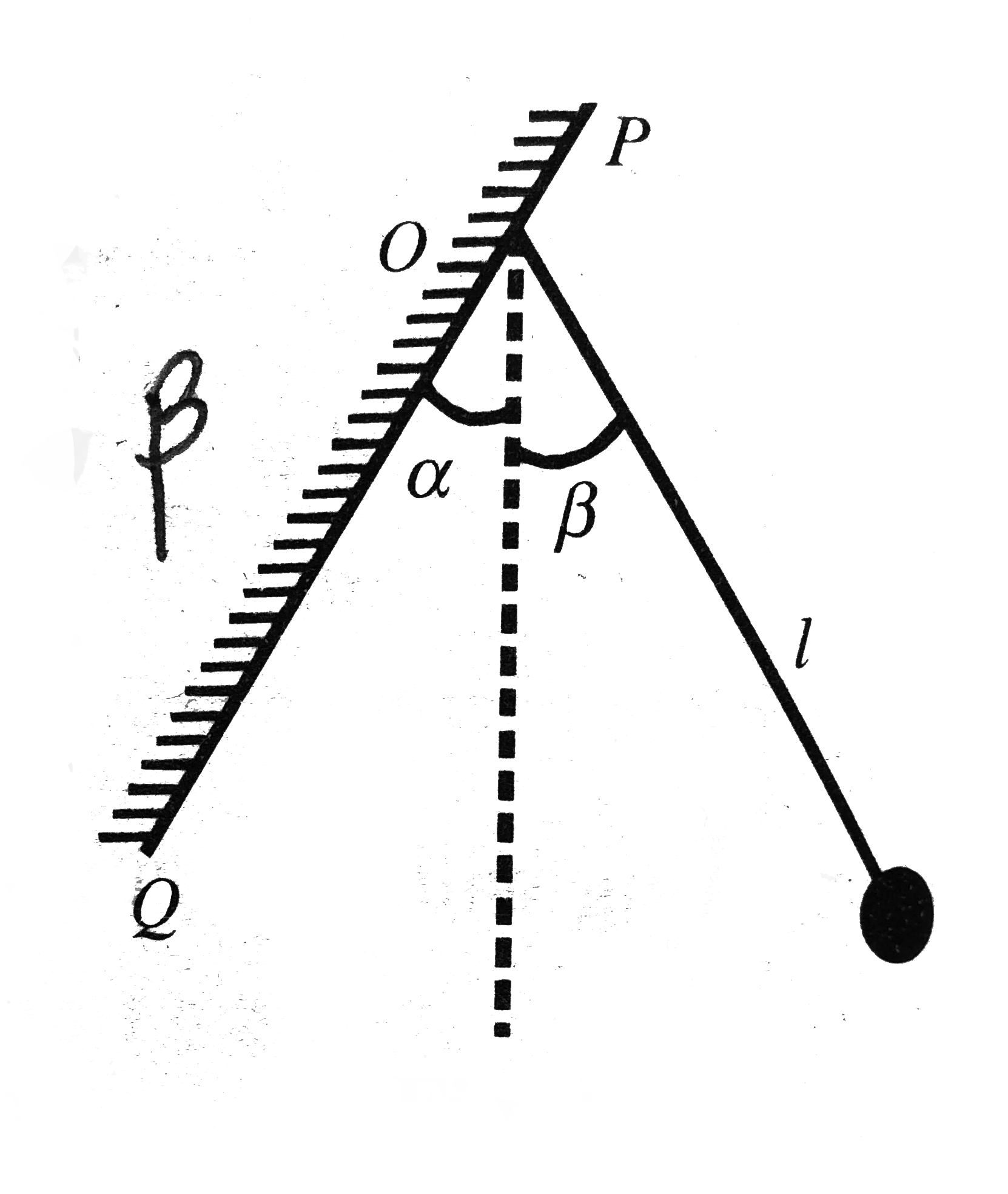
a. α>β
b. α<β
Assuming that any impact between the wall and the ball is elastic.
View SolutionA particle tide to the end of a string oscillates along a circular arc in a vertical plane. The other end of the string is fixed at the center of the circle. If the string has a breaking strength of twice the weight of the particles,
a. find the maximum distance that the particle can cover in one cycle of oscillation. The length of the string is 50cm.
b. Find the tension in the extreme position.
c. Find the acceleration of the particle at bottom and extreme position.
View SolutionA small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
View Solutiona small sphere of mass m susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical. (b) Find the angle θ between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
View Solution

