A square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
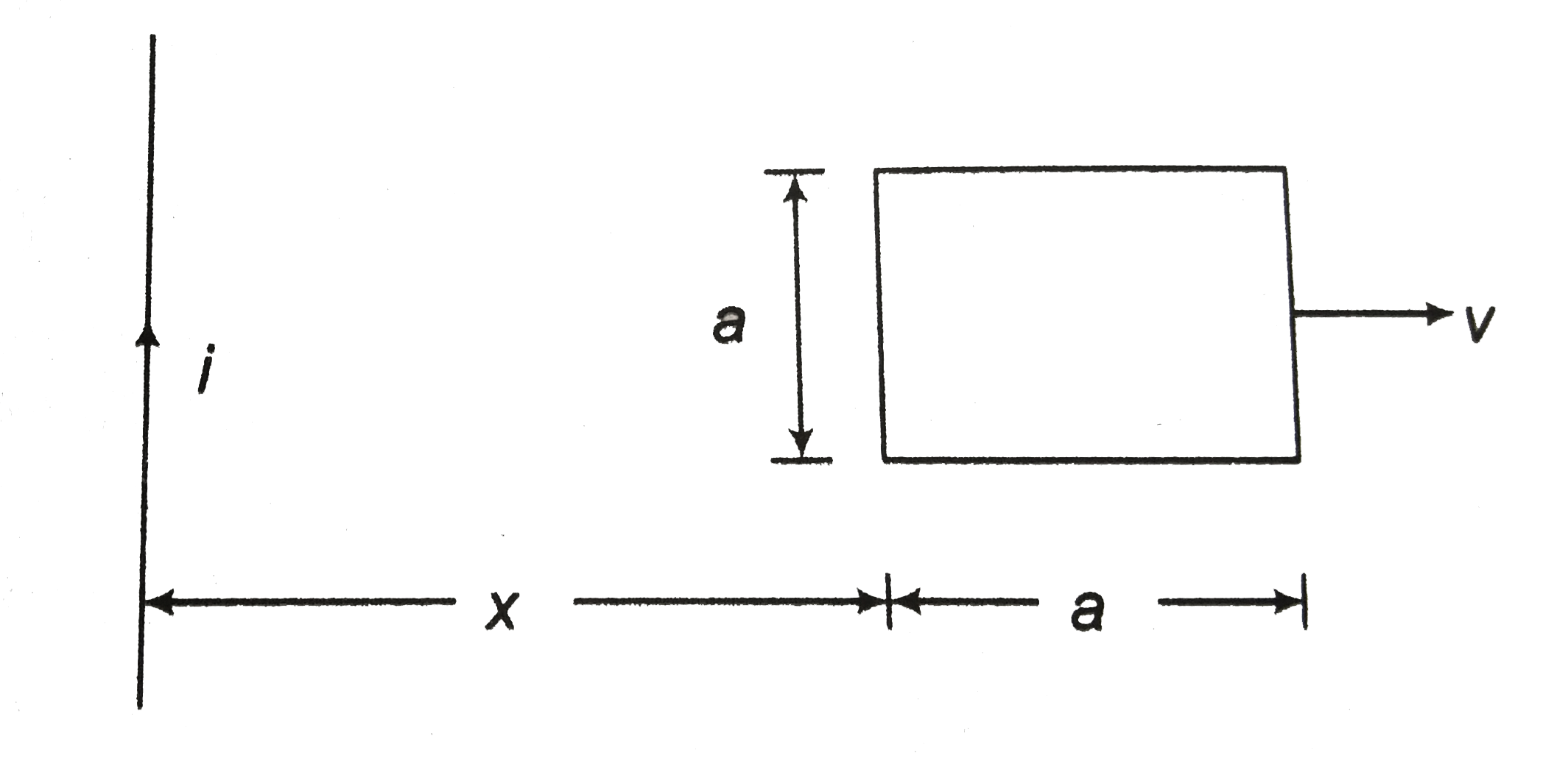
Field, due to the current carrying wire, at a perpendicular distance x from it is given by,
B(x)=μ02πix
Motional e.m.f is given by ∣∣∣∫−(→v×→B).d→l∣∣∣
There will be no induced e.m.f in the segments (2) and (4)
as, →v↑⏐⏐↑⏐⏐d→l and magnitude of e.m.f induced in 1 and 3, will be
ξ1=v(μ02πix)a and ξ2=v(μ02πi(a+x))a,
respectively, and thier sense will be in the direction of (→v×→B).
So, e.m.f., induced in the network =ξ1−ξ2[as ξ1>ξ2]
=avμ0i2π[1x−1a+x]=va2μ0i2πx(a+x)
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
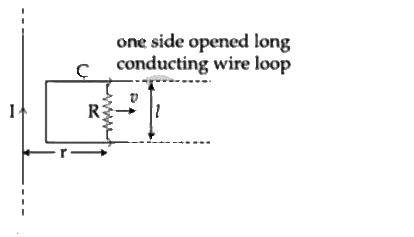
A long straight wire carrying a current I and a II- shaped conductor with siding connector are located in the same plane as shown in Fig. The connector of length l and resistance R sides to the right with a current induced in the loop as a function of separation r between the connector and the stragiht wire. The resistance of the II-shaped conductor and the self-induced of the loop are assumed to be negligible.

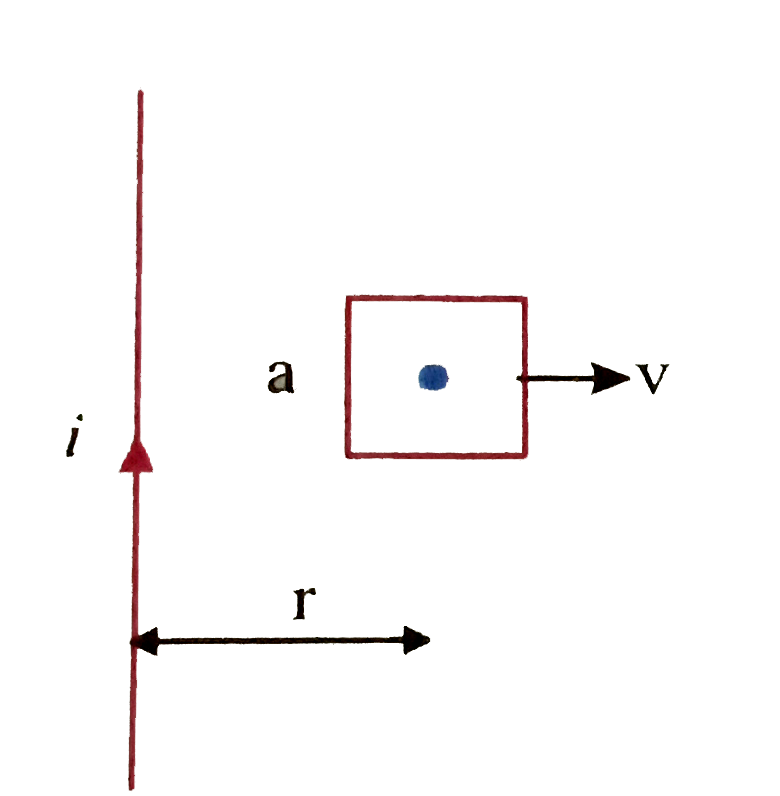
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View Solution
Knowledge Check
A conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
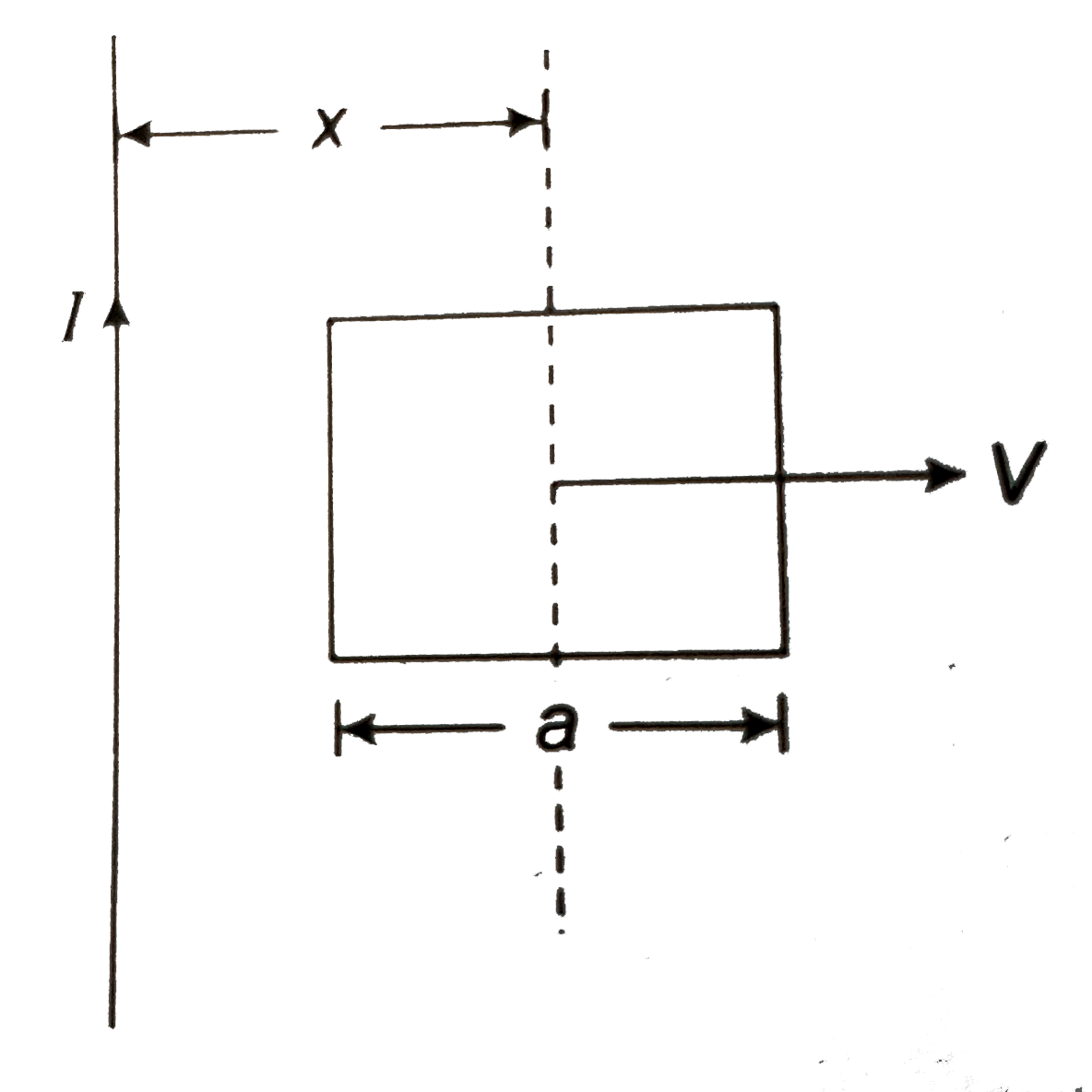 A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2
A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2A square frame of side 10 cm and a long straight wire carrying current 1 A are in the plane of the paper. Starting from close to the wire, the frame moves towards the right with a constant speed of 10ms−1 (sec figure). The e.m.f induced at the time the left arm of the frame is at x = 10 cm from the wire is
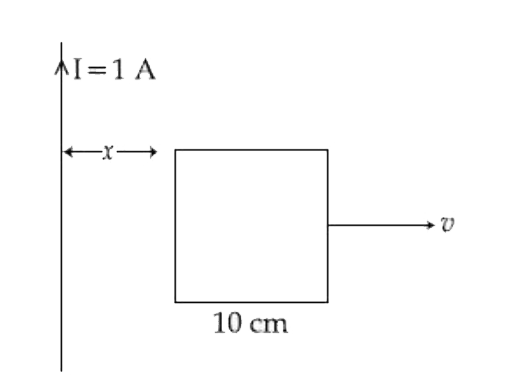 A0.75μvB1μvC2μvD0.5μv
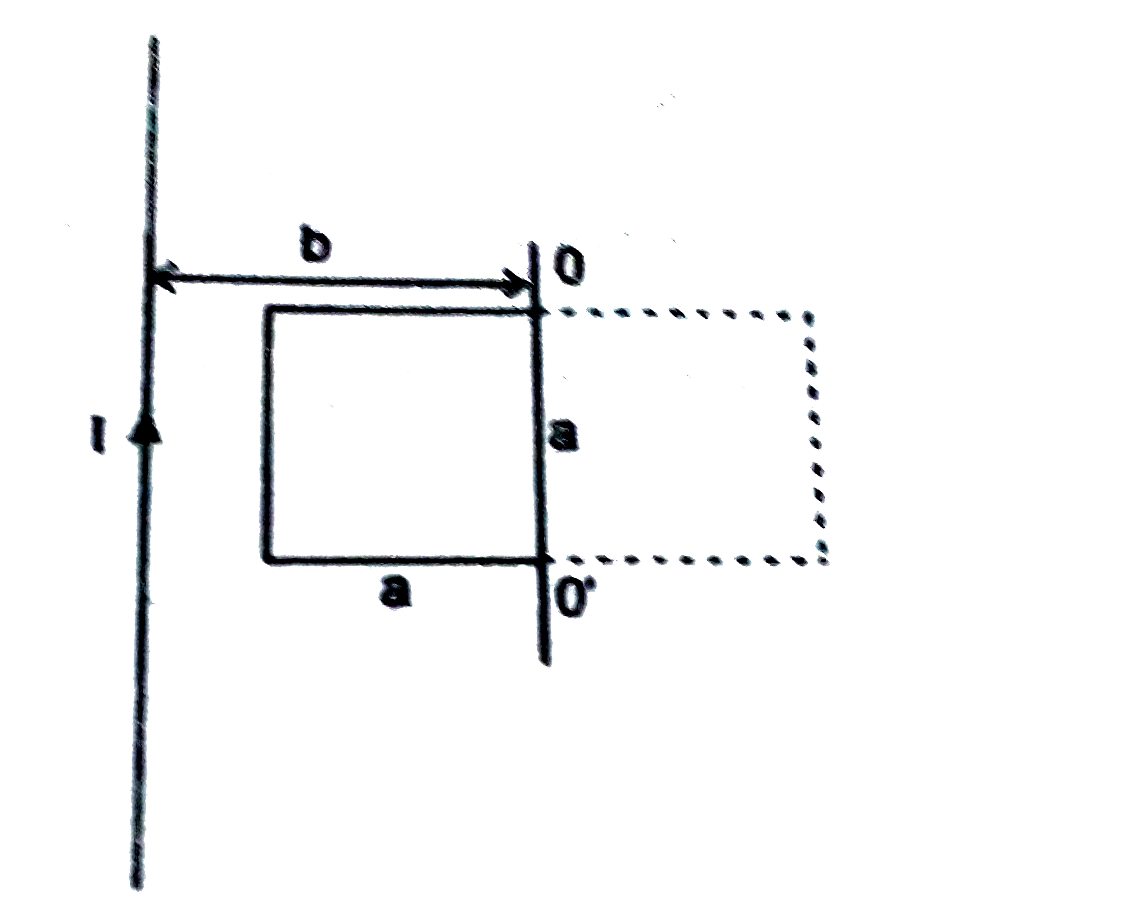
A0.75μvB1μvC2μvD0.5μvA square frame with side 'a' and a straight conductor carrying a constant current I are located in the same plane. The resistance of the frame is equal to R. The frame was turned through 180∘ about the axis OO' separated from the current-carrying conductor by a distance b=2a. If the electric charge that flowed through the frame be expressed as a function of a,I,R it takes the form q=constant ×am×In×Rp. Find m+n+p.
A1B2C3D4
A square wire frame with side a and a straight conductor carrying constant current I are located in the same plane (Fig). The inductance and the resitance of the frame are equal to L and R respectively. The frame was turned throgh 180∘ about the axis OO'separated fromt the current carrying conductor by a distance b. FInd the electric charge having flown through the frame.

View SolutionA sqare frame with side a=5 cm and a , long straight conductor carrying steady current I=5 A are located in the same plane . The inductance and the resistance of the frame are L=0.1 mH and R=1Ω. The frame is turned suddenly through 180 about the side parallel to the conductor which is at a distance b=10 cm .Find the charge through the frame .

View SolutionA Square frame with side a and a straigh conductor carrying a constant current I and located in the same plane. The inductance and the resistance of the frame are equal to L and R respectivaly. The frame was truned through I80∘ about the axis OO' separated from the current carrying conductor by a distance b . Find the electric charge having flown through the frame.

View SolutionA square wire frame ( initially current is zero) with side a and a straight conductor carrying a constant current I are located in the same plane (figure). The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 180∘ about the axis OO' separated from the current - carrying conductor by a distance b=2a. The total electric charge having flown through the frame if i=0 at t=0 in the loop is equal to μ0aI2πRlnx. Find the value of x.
View SolutionAn infinitely long straight wire carrying current I , one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane , as shown in the figure. The connector has length l and resistance R . It slides of the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible . The induced current in the loop , as function of separation r between the conductor and the straight wire is :
View Solution
