The system differs from the one examined in the foregoing problem (Fig ) by a capacitor of capacitance $C$ replacing the resistance $R$ . Find the accelearation of the connector.

Video Solution

Text Solution

Verified by Experts

From Lenz's law, the current the copper bar is directed from 1 to 2 or in other words, the induced current in the current is in clockwise sense.
Potential difference across the capacitor plates,
$\frac{q}{C} ξ_{in}$ or, $q = C ξ_{in}$

Hence, the induced current in the loop,
$i = \frac{d q}{d t} = C \frac{d ξ_{i n}}{d t}$
But the variation of magnetic flux through the loop is caused by the movement of the bat.
So, the infuced $e . m . f ., ξ_{i n} = B l v$
and, $\frac{d ξ_{i n}}{d t} = B l \frac{d v}{d t} = B l w$
Hence, $i = C \frac{d ξ}{d t} = C B l w$
Now, the forces acting on the bars are the weight and the Ampere's force, where $F_{a m p} = i l B (C B l w) B = C l^{2} B^{2} w$ .
From Newton's second law, for the rod, $F_{x} = m w_{x}$
or, $m g \sin α - C l^{2} B^{2} w = m w$
Hence $w = \frac{m g \sin α}{C l^{2} B^{2} + m} = \frac{g \sin α}{1 + \frac{l^{2} B^{2} C}{m}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
As in the figure, if a capacitor of capacitance 'C' is charged by connecting it with resistance R, then energy given by the battery will be

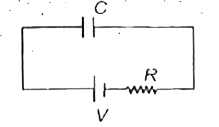A $\frac{1}{2} C V^{2}$
Bless than $\frac{1}{2} C V^{2}$
C $C V^{2}$
DMore than $C V^{2}$
Question 2 - Select One or More
A capacitor of capacitance $C_{1}$ is charged to a potential difference V and then connected with an uncharged capacitor of capacitance $C_{2}$ a resistance R. The switch is closed at t = 0. Choose the correct option(s):
AThe initial current through the resistance is $\frac{V}{R}$
BThe current through the resistance as a function of time is $i (t) = \frac{V}{R} e^{- \frac{t}{τ}}$ where $τ = R (\frac{C_{1} C_{2}}{C_{1} + C_{2}})$
CThe charge on capacitor $C_{1}$ as a function of time is $q_{1} (t) = (\frac{C_{1} V}{C_{1} + C_{2}}) (C_{1} + C_{2} e^{- \frac{t}{τ}})$
DAfter a long time, the potential difference across the capacitor $C_{1} i s (\frac{C_{1}}{C_{1} + C_{2}}) V$
Question 3 - Select One
circuit consists of a source of EMF $ξ$ and internal resistance r, two capacitors each of capacitance C and two resistors, each of value R. The voltage across either capacitor is:

A $\frac{ξ R}{2 (R + r)}$
B $\frac{ξ R}{(R + r)}$
C $\frac{ξ (R + r)}{2 R}$
DZero

IE IRODOV, LA SENA & SS KROTOV-ELECTRODYNAMICS-Electromagnetic Induction

Home
Ask Doubt
Profile