A square wire frame with side a and a straight conductor carrying constant current I are located in the same plane (Fig). The inductance and the resitance of the frame are equal to L and R respectively. The frame was turned throgh 180∘ about the axis OO'separated fromt the current carrying conductor by a distance b. FInd the electric charge having flown through the frame.

According to Ohm's law and Faraday's law of induction, the current i0 appearing in the frame, during its rotation is determind by the formula,
i0=dΦdt=I.di0dt
Hence, the required amount of electricity (charge) is,
q=∫i0dt=1R∫(dΦ+Ldi0)=−1R(ΔΦ+LΔi0)
Since the frame has been stopped after rotations, the current in it vanishes, and hence Δi0=0. It remains for us to find the increment of the flux ΔΦ through the frame (ΔΦ−Φ2−Φ1).
Let us choose the normal →n to the plane of the frame, for instane, so that is the final position, →n is directed behind the plane of the figure (along →B).
Then it can be easily seen that in the final position, Φ2>0, while in the initial position, Φ1<0 (the normal is opposite to →B) and ΔΦ turns out to be simply equal to the fulx throgh the surface bounded by the final and initial positions of the frame :
ΔΦ=Φ2+|Φ1|=∫b+ab−aBadr,
where B is a function of r, whose from can be easily found with the help of the theorem of circulation. Finally omitting the minus sign, we obtain,
q=ΔΦR=μ0ai2πR In b+ab−a

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A square wire frame ( initially current is zero) with side a and a straight conductor carrying a constant current I are located in the same plane (figure). The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 180∘ about the axis OO' separated from the current - carrying conductor by a distance b=2a. The total electric charge having flown through the frame if i=0 at t=0 in the loop is equal to μ0aI2πRlnx. Find the value of x.
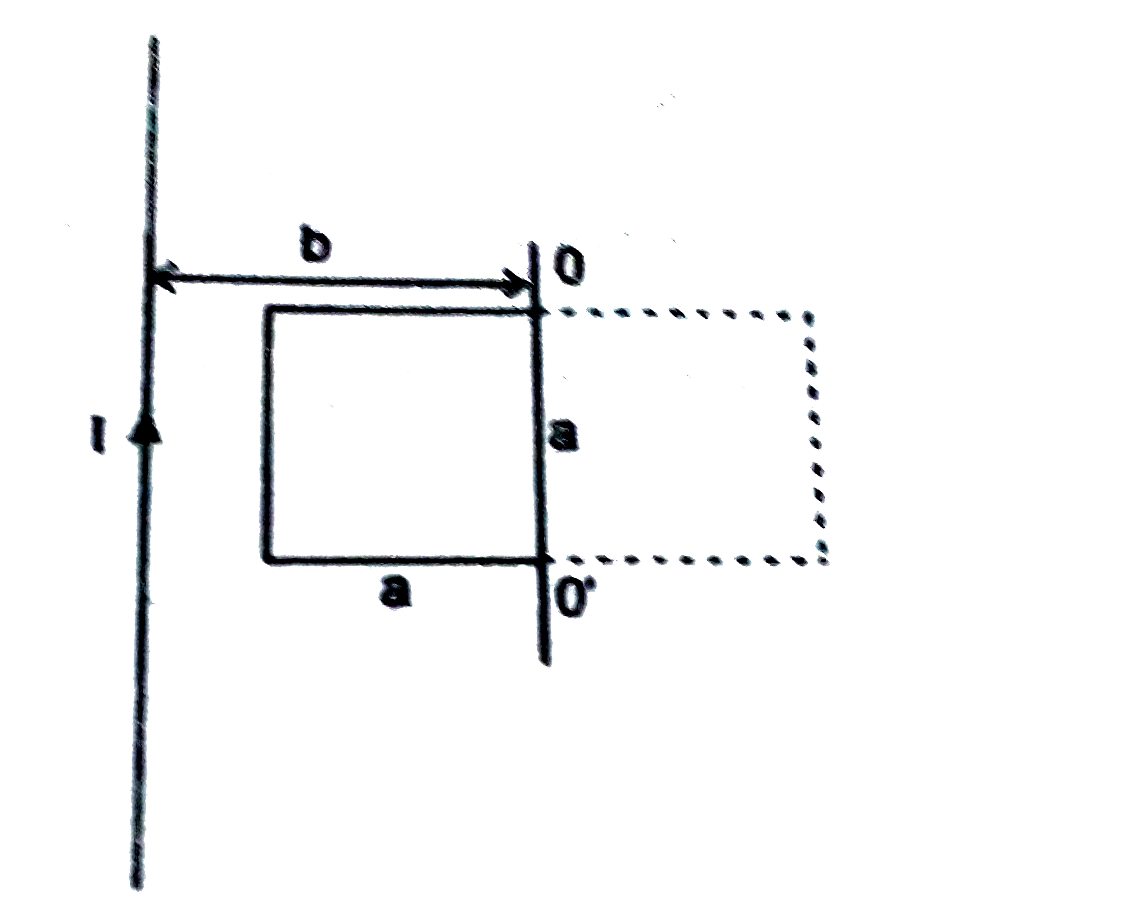
View SolutionA Square frame with side a and a straigh conductor carrying a constant current I and located in the same plane. The inductance and the resistance of the frame are equal to L and R respectivaly. The frame was truned through I80∘ about the axis OO' separated from the current carrying conductor by a distance b . Find the electric charge having flown through the frame.

View Solution
Knowledge Check
A square frame with side 'a' and a straight conductor carrying a constant current I are located in the same plane. The resistance of the frame is equal to R. The frame was turned through 180∘ about the axis OO' separated from the current-carrying conductor by a distance b=2a. If the electric charge that flowed through the frame be expressed as a function of a,I,R it takes the form q=constant ×am×In×Rp. Find m+n+p.
A1B2C3D4A conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
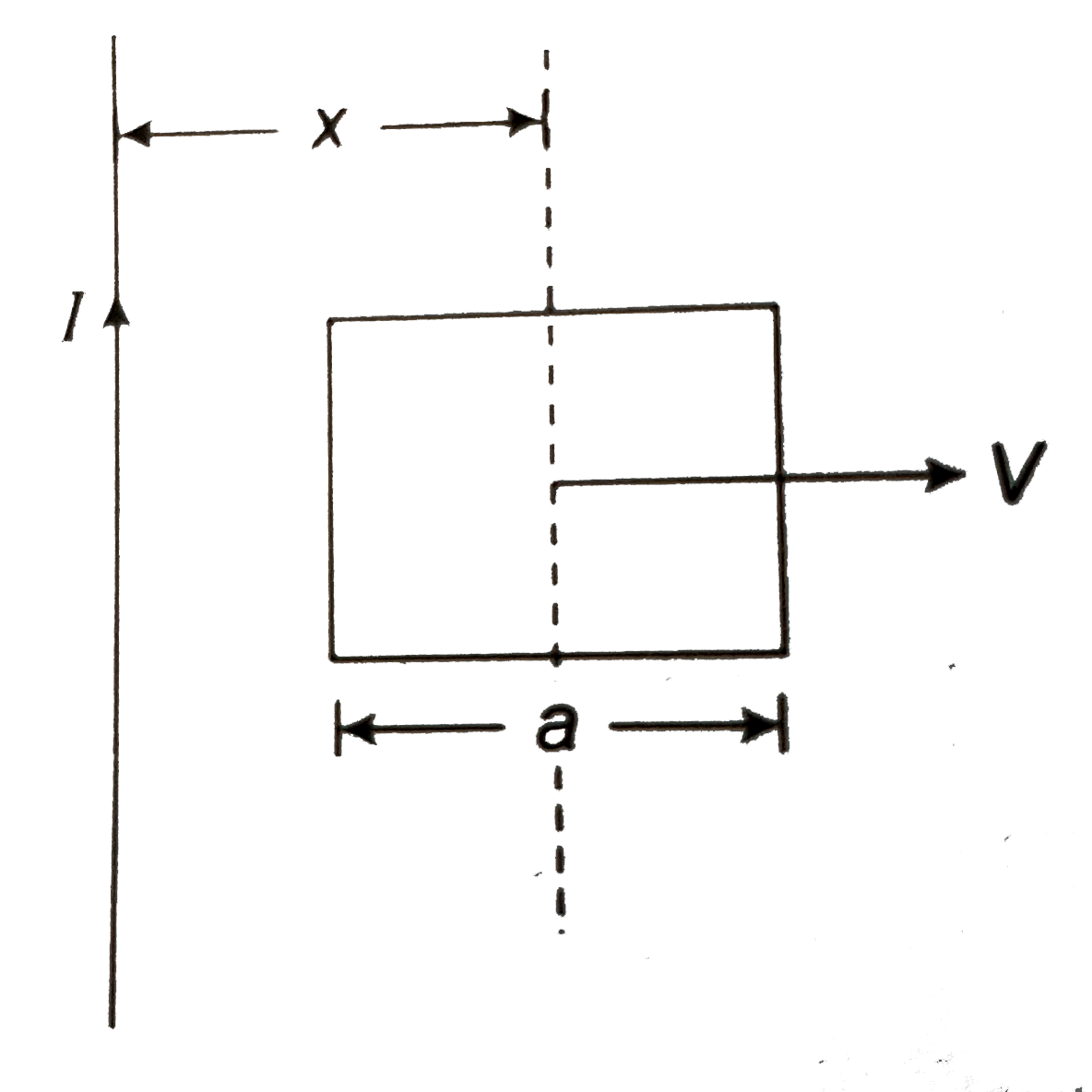 A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2
A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2A straight wire carrying current is parallel to the y-axis as shown in Fig. The
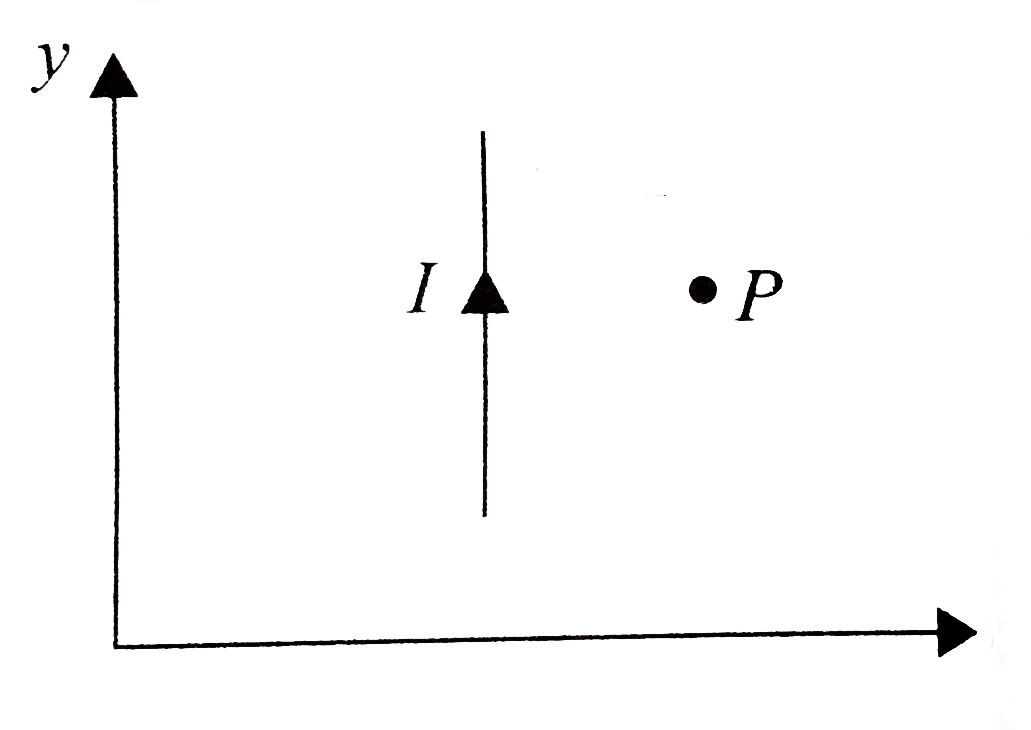 Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.
Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.
A sqare frame with side a=5 cm and a , long straight conductor carrying steady current I=5 A are located in the same plane . The inductance and the resistance of the frame are L=0.1 mH and R=1Ω. The frame is turned suddenly through 180 about the side parallel to the conductor which is at a distance b=10 cm .Find the charge through the frame .

View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
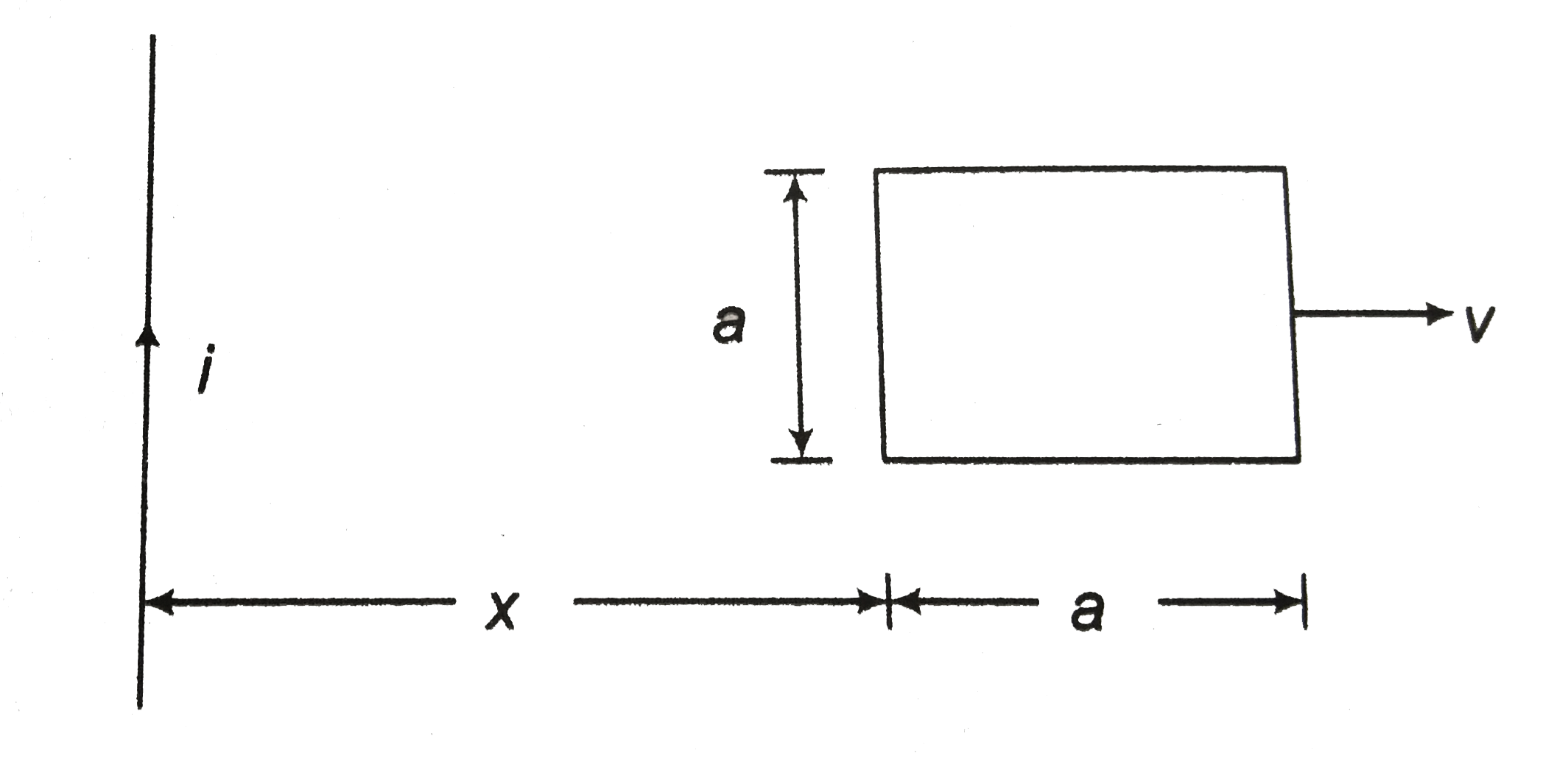
View Solution
A square loop ABCD carrying a current i is placed near and coplanar with a long straight conductor XY carrying a current I.
View SolutionA square loop of side as and a straight long wire are placed in the same plane as shown in figure. The loop has a resistance R and inductance L. The frame is turned through 180∘ about the axis OO′. What is the electric charge that flows through the loop?

View SolutionA square loop ABCD , carrying a current I, is placed near and coplanar with a long straight conductor XY carrying a current I.

View Solution

