A wire shaped as a semi-circle of radius a rotates about sn sxis OO' with an angular velocity ω in a unifrom magnetic field of induction B' (Fig). The rotation axis is perpendicular to the field direction. The total resistance of the circuit is equal to R. NEglecting the magnetic field of the induced current, find the meand amount of thermal power being generated in the loop fueing a rotation period.
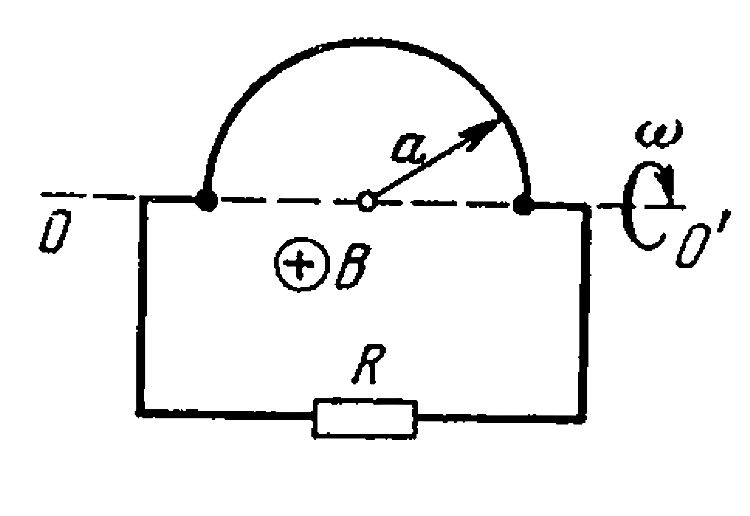
Flux of →B, at an orbitarty moment of time t :
Φt=→B.→S=Bπa22cosωt,
From Faraday's law, induced e.m.f.,ξIn=dΦdt
=−d(Bπa22cosωt)dt=Bπa2ω2sinωt.
and induced current, iin=ξinR=Bπa22Rωsinωt.
Now thermal power, generated in the circuit, at the moment t=t :
p(t)=ξin×iin=(Bπa2ω2)21Rsin2ωt
and mean thermal power generated,
<P>=[Bπa2ω2]21R∫T0sin2ωtdt∫T0dt=12π(πa2B2)2
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
Knowledge Check
A horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
AzeroBπr2ωBC12Br2ωDBr2ωA wire loop is rotated in a uniform magnetic field about an an axis perpendicular to the field. The direction of the current induced in the loop reverses once each
Aquarter revolutionBhalf revolutionCfull revolutionDtwo revolutionsA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
A(a) The emf will be maximum at the moment when flux is zeroB(b) The emf will be 0 at the moment when flux ismaximumC( c) The emf will be maximum at the moment when plane of the loop is parallel to the magnetic fieldD(d) The phase difference between the flux and the emf π/2
A semicircular wire of radius R= 20 cm rotates in its own plance about one end with angular velocity w=10rad/s in unifornm magnetic field B=5 mT perpendicular into the plane of the wire gtFind the voltage developend between the ends of the wire
View SolutionA circular wire of radius r rotates about its own axis with angular speed w in a magnetic field B perpendicular to its plane, then the induced e.m.f. is
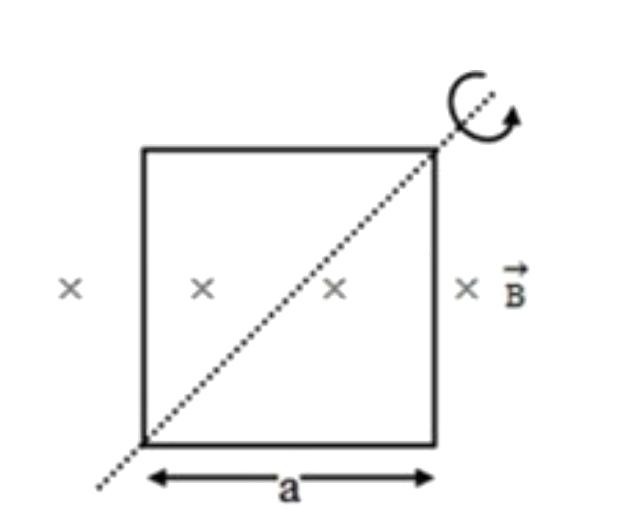
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionA wire loop is rotated in a uniform magnetic field about an axis perpendicular to the field. The direction of the current induced in the loop reverses in each
View SolutionA wire shaped as a semicircle of radius a, is rotating about an acis PQ with a constant angular velocity ω=1√LC, with the help of an external agent. A uniform magnetic field B exists in space and is directed into the plane of the figure. (circuit part remains at rest) (left part is at rest)

View Solution

