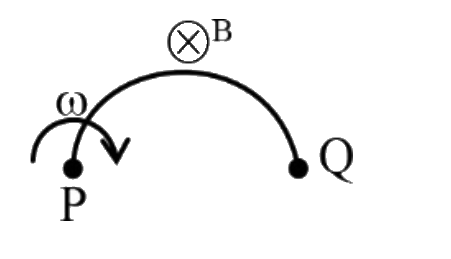
A wire shaped as a semicircle of radius a, is rotating about an acis PQ with a constant angular velocity $ω = \frac{1}{\sqrt{L C}}$ , with the help of an external agent. A uniform magnetic field B exists in space and is directed into the plane of the figure. (circuit part remains at rest) (left part is at rest)

The rms value of current in the circuit is $\frac{π B a^{2}}{R \sqrt{2 L C}}$

The rms value of current in the circuit is $\frac{π B a^{2}}{2 R \sqrt{2 L C}}$

The maximum energy stored in the capacitor is $\frac{π^{2} B^{2} a^{4}}{8 R^{2} C}$

The maximum power delivered by the external agent is $\frac{π^{2} B^{2} a^{4}}{4 L C R}$

Video Solution

Text Solution

Verified by Experts

Let at time t the angle between magnetic field and area vector (semicircle) be $θ$ , then $θ = w t$
$ϕ = \to B . \to S = \frac{π a^{2} B}{2} cos ω t$ .
$ε = - \frac{d ϕ}{d t} = \frac{π B a^{2} ω}{2} sin ω t$
$ε_{0} = \frac{π B a^{2}}{2 \sqrt{L C}}$ peak emf
Since the circuit is in resonance
$| z | = R \Rightarrow i_{0} = \frac{π B a^{2}}{2 R \sqrt{L C}}$ peak current
$i_{r m s} = \frac{i_{0}}{\sqrt{2}} \Rightarrow i_{r m s} = \frac{π B a^{2}}{2 R \sqrt{2 L C}}$
$U_{C} = \frac{1}{2} C V_{0}^{2} \to$ max. energy $V_{0} \to$ peak voltage
$V_{0} = i_{0} X_{c} = \frac{i_{0}}{C ω} = \frac{i_{0} \sqrt{L C}}{C}$
$U_{C} = \frac{1}{2} C \times \frac{π^{2} B^{2} a^{4}}{4 R^{2} C^{2}} = \frac{π^{2} B^{2} a^{4}}{8 R^{2} C}$
$P_{e x t} . = P_{Dissipated} = ε_{0} i_{0} = \frac{π B a^{2}}{2 \sqrt{L C}} \times \frac{π B a^{2}}{2 R \sqrt{L C}}, P_{E x t} = \frac{π^{2} B^{2} a^{4}}{4 L C R}$

Updated on:21/07/2023