A series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:

zero in both

maximum in both

zero & maximum respectively

maximum & zero respectively

Video Solution

Text Solution

Verified by Experts

$\frac{d q}{d t} = i = 0 Q \to max$
$E_{c} = \frac{Q^{2}}{2 c} \Rightarrow max$
$E_{L} = \frac{L i^{2}}{2} \Rightarrow z e r o$

Updated on:21/07/2023

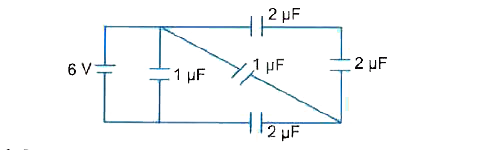
In the circuit shown, the energy stored in $1 μ F$ capacitor is
A $40 μ J$
B $64 μ J$
C $32 μ J$
Dnone of these
The series $R L C$ circuit in resonance is called:
ASelector circuit
Brejector circuit
Camplifier circuit
Doscillator circuit
In a series circuit $C = 2 μ F, L = 1 m H$ and $R = 10 Ω$ , when the current in the circuit is maximum, at that time the ratio of the energies stored in the capacitor and the inductor will be
A $1 : 1$
B $1 : 2$
C $2 : 1$
D $1 : 5$