A rectangular loop of sides of length l and b is placed in x-y plane. A uniform but time varying magnetic field of strength →B=20tˆi+10t2ˆj+50ˆk where t is time elapsed. The magnitude of induced emf at time t is:
20+20t
20
20t
zero
To solve the problem, we need to find the induced electromotive force (emf) in a rectangular loop placed in a time-varying magnetic field. The magnetic field is given by:
→B=20t^i+10t2^j+50^k
Step 1: Determine the area vector of the rectangular loop
The rectangular loop lies in the x-y plane, which means its area vector →A will be perpendicular to the plane of the loop. For a loop with sides of length l and b, the area vector can be expressed as:
→A=l⋅b^k
Step 2: Calculate the magnetic flux through the loop
The magnetic flux Φ through the loop is given by the dot product of the magnetic field →B and the area vector →A:
Φ=→B⋅→A
Substituting the values:
Φ=(20t^i+10t2^j+50^k)⋅(l⋅b^k)
Since the dot product only considers the component along ^k:
Φ=50⋅(l⋅b)
Step 3: Determine the induced emf
The induced emf (E) in the loop can be calculated using Faraday's law of electromagnetic induction, which states that the induced emf is equal to the negative rate of change of magnetic flux through the loop:
E=−dΦdt
Step 4: Evaluate the time derivative of the magnetic flux
Since we have found that:
Φ=50lb
This expression is a constant (it does not depend on time t). Therefore, the time derivative of Φ is:
dΦdt=0
Step 5: Calculate the induced emf
Substituting this result back into the equation for induced emf:
E=−dΦdt=−0=0
Thus, the magnitude of the induced emf at time t is:
E=0V
Final Answer
The magnitude of the induced emf at time t is 0 V.
---
The rectangular loop lies in the x-y plane, which means its area vector →A will be perpendicular to the plane of the loop. For a loop with sides of length l and b, the area vector can be expressed as:
The magnetic flux Φ through the loop is given by the dot product of the magnetic field →B and the area vector →A:
The induced emf (E) in the loop can be calculated using Faraday's law of electromagnetic induction, which states that the induced emf is equal to the negative rate of change of magnetic flux through the loop:
Since we have found that:
Substituting this result back into the equation for induced emf:
The magnitude of the induced emf at time t is 0 V.
Topper's Solved these Questions
Similar Questions
The position vector of a particle changes with time according to the relation →r(t)=15t2ˆi+(4−20t2)ˆj What is the magnitude of the acceleration at t = 1?
View SolutionA wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field →B=(2ˆi−3ˆj+ˆk)T is present in the region. Then, find
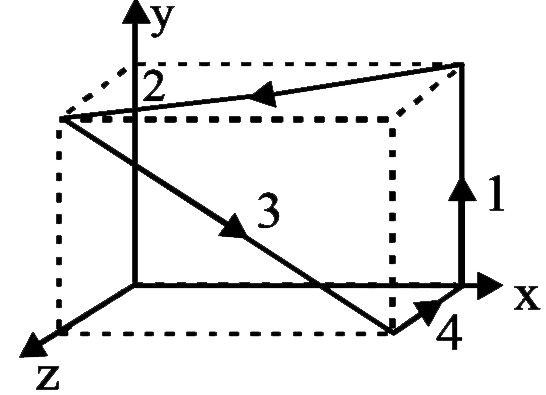
The net torque on the loop
View Solution
Knowledge Check
A rectangular loop of sides a and b is placed in xy-placed. A uniform but time varying magnetic field of strength B=20tˆi+10t2ˆj+50ˆk is present in the region. The magnitude of induced emf in the loop at time t is
A20+20tB20C20tDzeroA rectangular loop os sides of length l an db is placed in x-y plane. A uniform but it me varying manetic field of strength exists in space. The magnitude of induced e.m.f. at time t is:
A20+20tB20C20tDnone of the aboveA reacangular loop if size (2m×1m) is placed in x-y plane. A uniform but time varying magnetic field of strength T where t is the time elsapsed in second exists in sosace. The magnitude of induced emf (in V) at time t is
A20=20iB20C20iDzero
A point on the line →r=2ˆi+3ˆj+4ˆk+t(ˆi+ˆj+ˆk) is
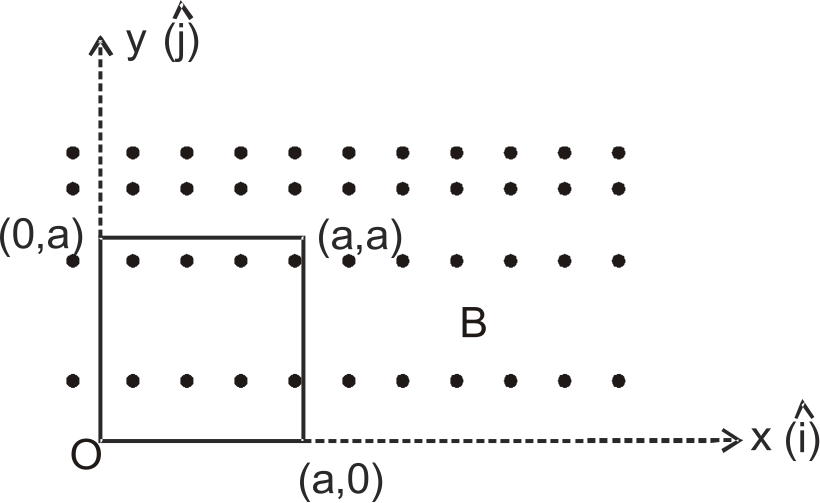
View SolutionA square loop of side 'a' is placed in x−y plane as shown in figure. In this region there is non-uniform time dependent magnetic field →B=(cy3t2)→k, [where t is time and c is constant] then magnitude of emf induced in loop is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
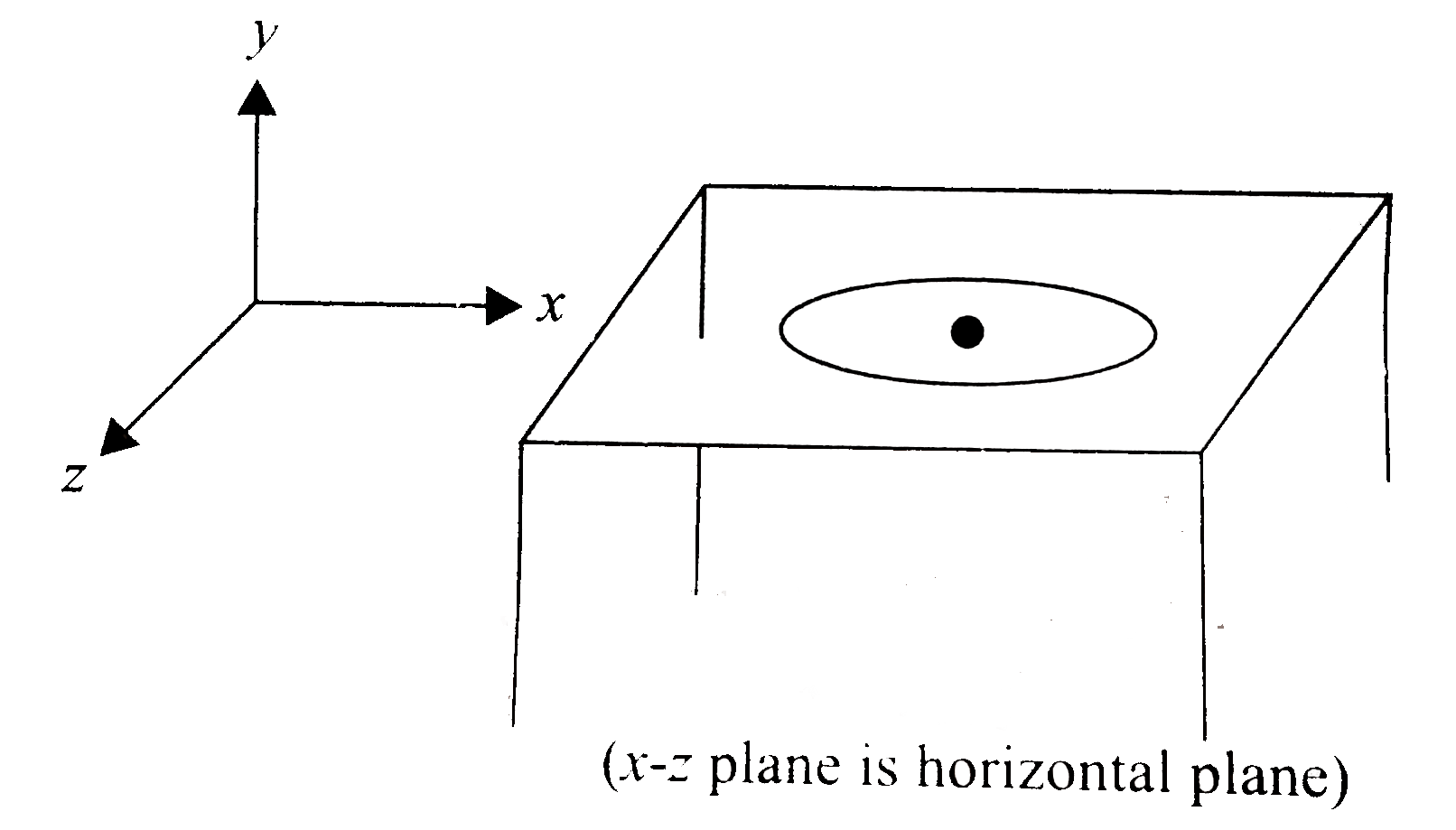
Net magnetic field (in Newton) on conducting ring as function of time is
View SolutionA magnet of magnetic moment of 50 ˆiAm2 is placed along the x - axis in magnetic field →B=(0.5ˆi+3.0ˆj)T. The torque acting on the manet is
View SolutionA radius vector of point A relative to the origin varies with time t as →r=atˆi−bt2ˆj where aandb are constant. The equation of point's trajectory is.
View Solution
