A Square frame with side a and a straigh conductor carrying a constant current I and located in the same plane. The inductance and the resistance of the frame are equal to L and R respectivaly. The frame was truned through I80∘ about the axis OO' separated from the current carrying conductor by a distance b . Find the electric charge having flown through the frame. 
Magnetic field due to long wire
B=μ0I2πx,⊗
magnetic field is variable, taking a strip of length a and with dx
dA=adx
dϕ=−BdA−μ0Ia2πdxx
ϕ=−μ0Ia2π∫b(b−a)dxx=−μ0Ia2π|1nx|a(b−a)
=−μ0Ia2π[1n(b)−(b−a)]=−μ0Ia2π1n(bb−a)
ϕ'=μ0Ia2π∫b+abdxx
=μ0Ia2π1n(b+ab)
Change flown
Δq=ϕ'−ϕR=μ0Ia2πR1n(b+ab−a)

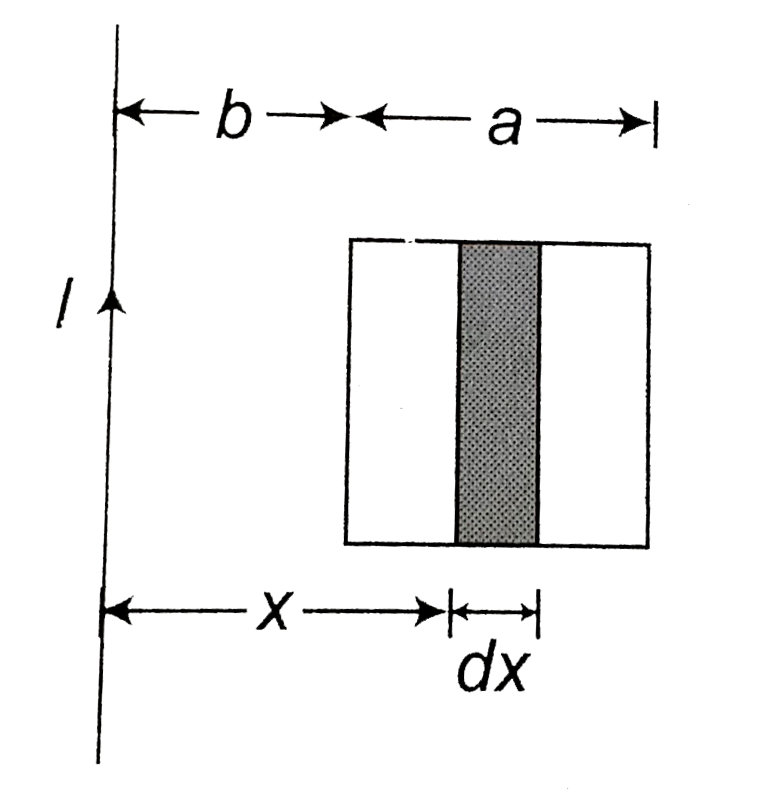
Topper's Solved these Questions
Similar Questions
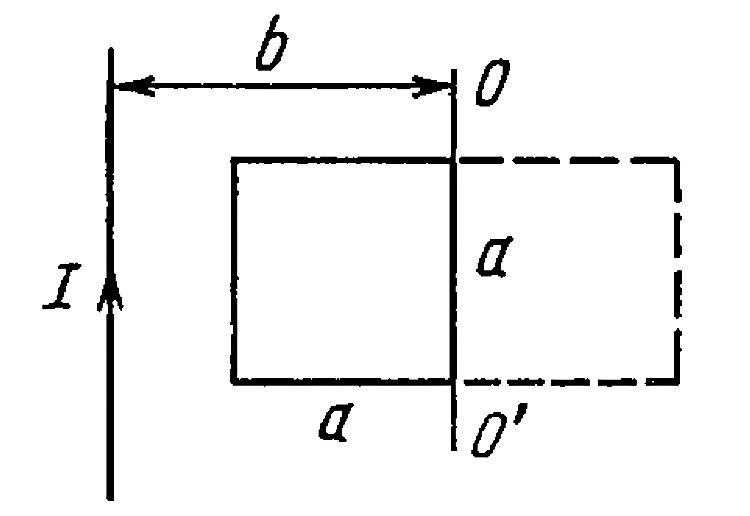
A square wire frame with side a and a straight conductor carrying constant current I are located in the same plane (Fig). The inductance and the resitance of the frame are equal to L and R respectively. The frame was turned throgh 180∘ about the axis OO'separated fromt the current carrying conductor by a distance b. FInd the electric charge having flown through the frame.
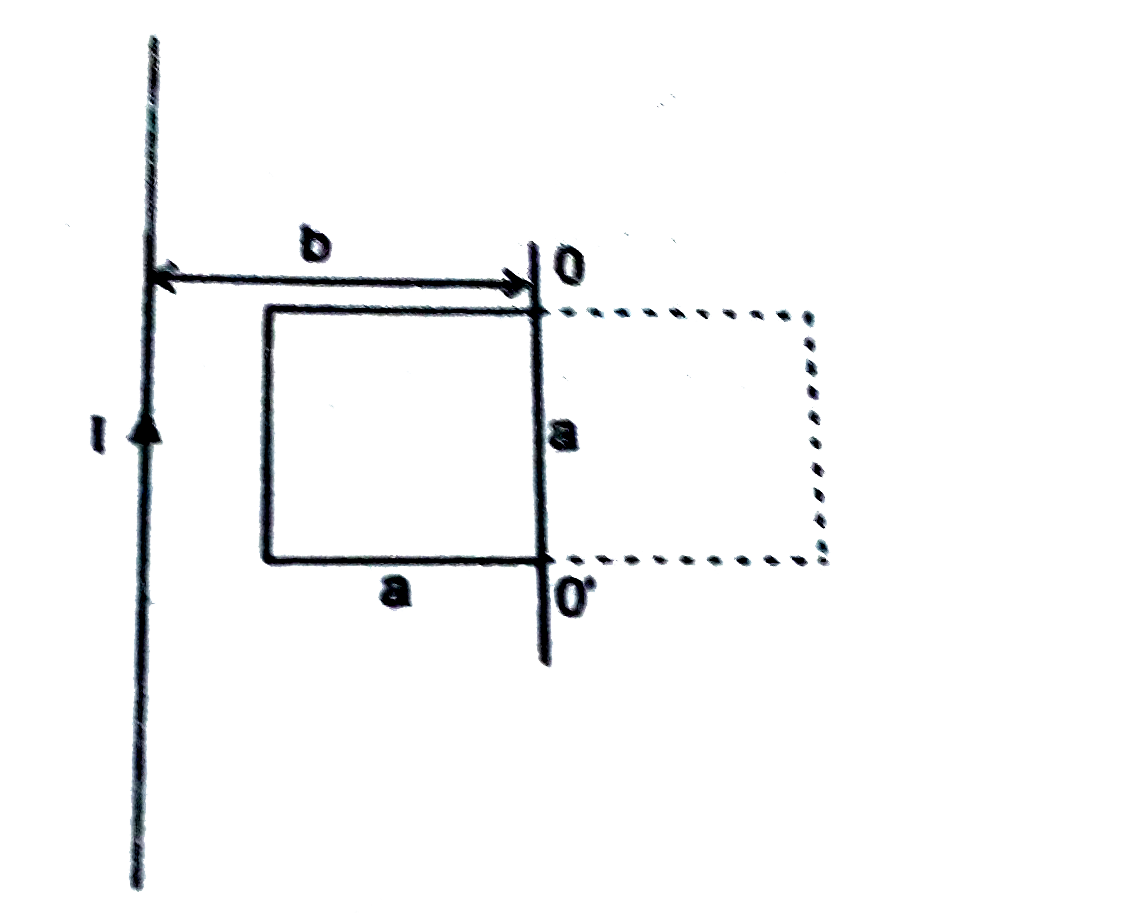
View SolutionA square wire frame ( initially current is zero) with side a and a straight conductor carrying a constant current I are located in the same plane (figure). The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 180∘ about the axis OO' separated from the current - carrying conductor by a distance b=2a. The total electric charge having flown through the frame if i=0 at t=0 in the loop is equal to μ0aI2πRlnx. Find the value of x.
View Solution
Knowledge Check
A square frame with side 'a' and a straight conductor carrying a constant current I are located in the same plane. The resistance of the frame is equal to R. The frame was turned through 180∘ about the axis OO' separated from the current-carrying conductor by a distance b=2a. If the electric charge that flowed through the frame be expressed as a function of a,I,R it takes the form q=constant ×am×In×Rp. Find m+n+p.
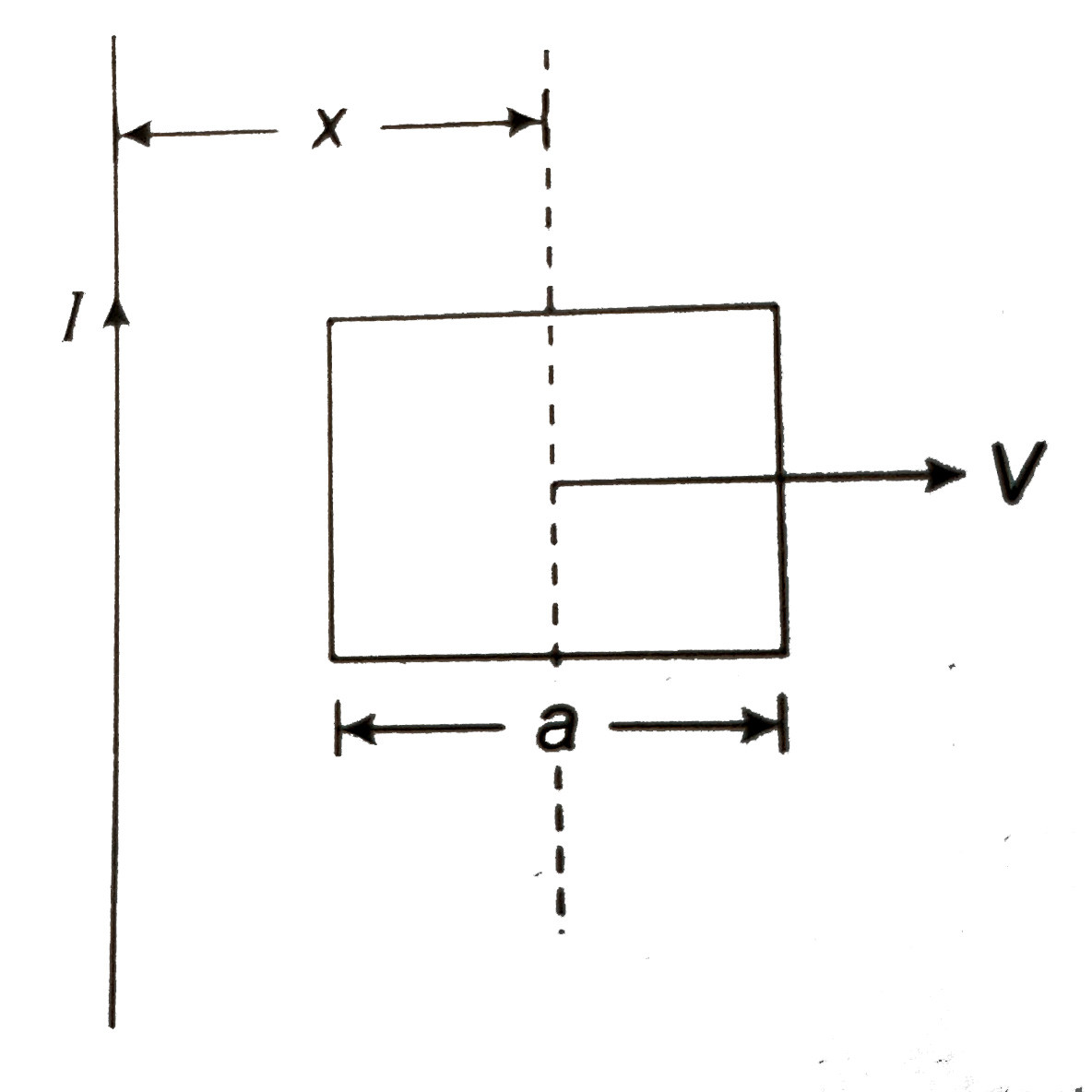
A1B2C3D4A conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
 A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2
A1(2x−a)2B1(2x+a)2C1(2x−a)(2x+a)D1x2A square loop of side as and a straight long wire are placed in the same plane as shown in figure. The loop has a resistance R and inductance L. The frame is turned through 180∘ about the axis OO′. What is the electric charge that flows through the loop?
 Aμ0Ia2πRln(2a+bb)Bμ0Ia2πRln(bb2−a2)Cμ0Ia2πRln(a+2bb)DNoneof these
Aμ0Ia2πRln(2a+bb)Bμ0Ia2πRln(bb2−a2)Cμ0Ia2πRln(a+2bb)DNoneof these
A sqare frame with side a=5 cm and a , long straight conductor carrying steady current I=5 A are located in the same plane . The inductance and the resistance of the frame are L=0.1 mH and R=1Ω. The frame is turned suddenly through 180 about the side parallel to the conductor which is at a distance b=10 cm .Find the charge through the frame .

View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
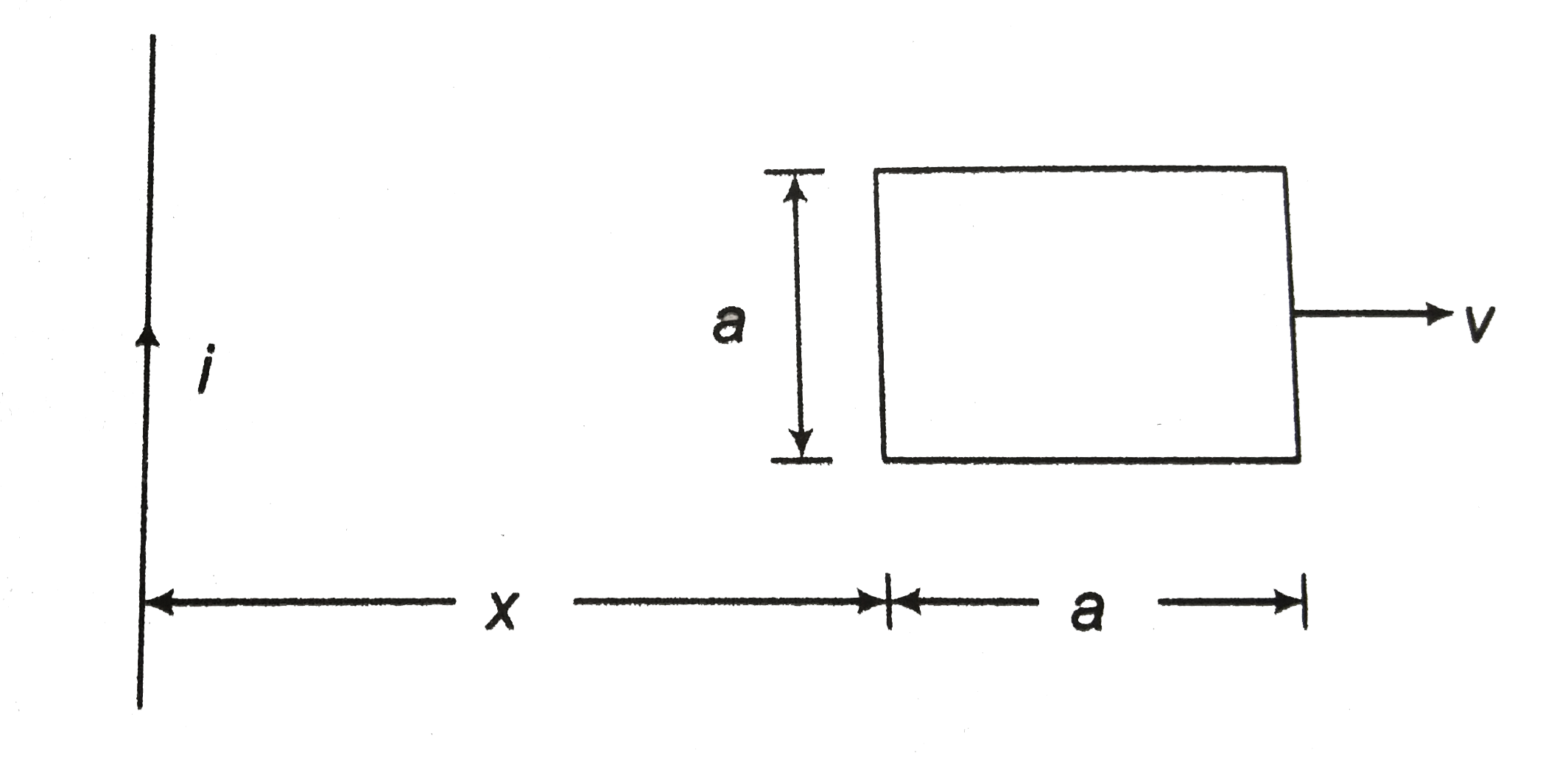
View SolutionFigure shows a square conducting frame and a long wire-both lying in the same plane. The side length of the square loop is ‘a’ and it is at a distance ‘a’ from the long wire which is having a steady current I0. The inductance and resistance of the square loop are L and R respectively. The loop is turned by 180° about its side AB so as to bring it to final position ABC'D' at rest. Calculate the net charge that flow past a side of the loop.
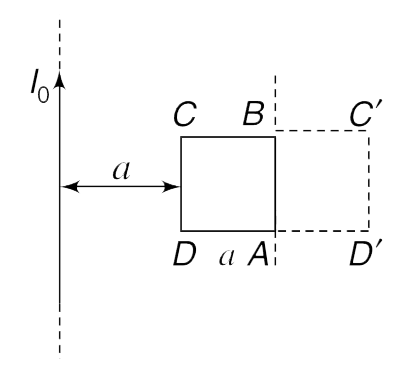
View SolutionA square frame carrying a current I is located in the same plane as a long straight wire carrying a current I0 The frame side has a length a. The axis of the frame passing through the midpoints of the opposite sides is parallel to the wire and is separated from it by the distance which is η times greater than the side of the frame. Find
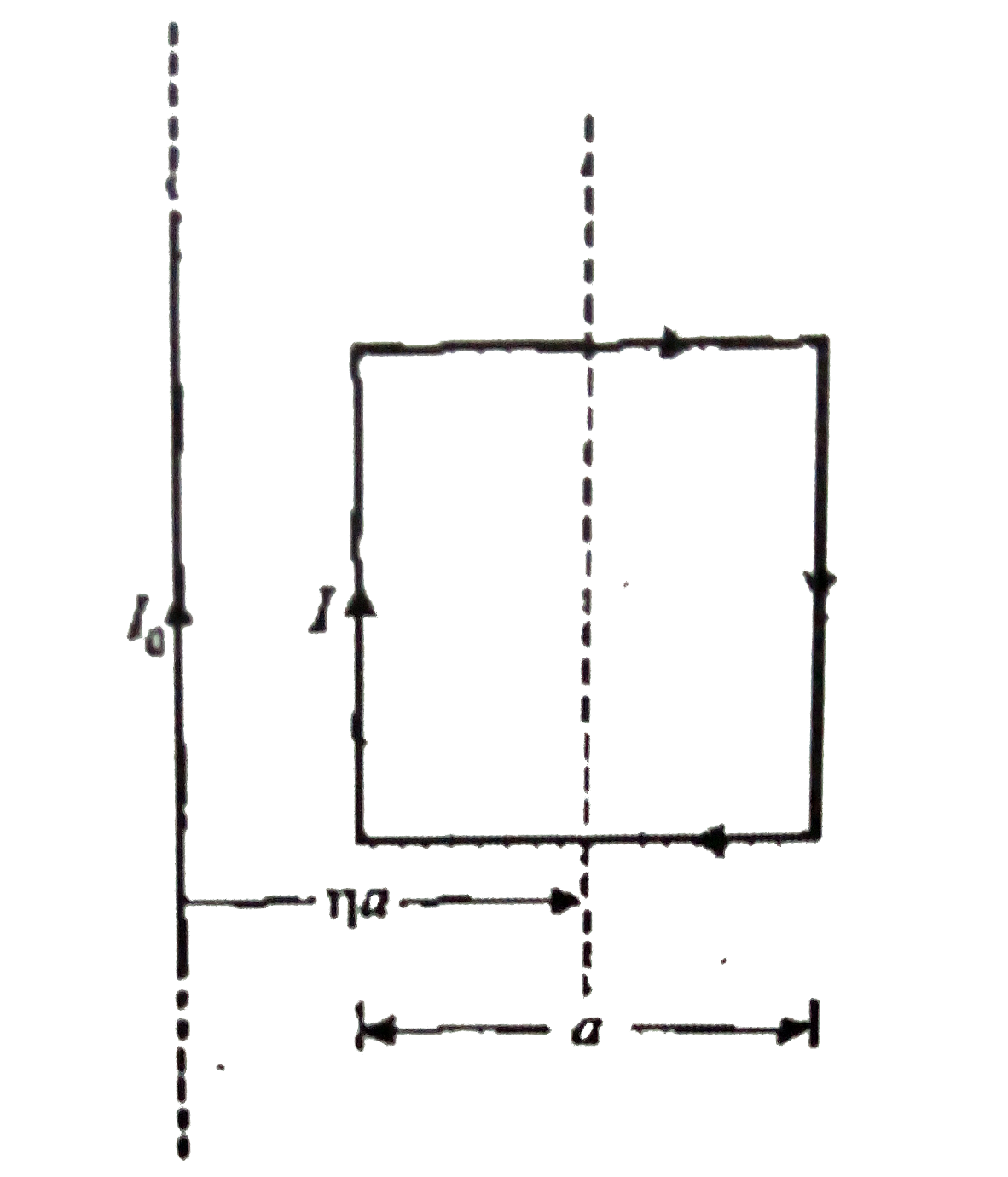
(a) Force acting on the frame
(b) The mechanical work to be performed in order to turn the frame through 180∘ about its axis, with the currents maintained constant.
View SolutionA hydrogen atom in the normal state is located at a distance r=2.5cm from a long straight conductor carrying a current I=10A. Find the maximum force acting on the atom.
View Solution
