A capacitor of capacitance C1 is charged to a potential difference V and then connected with an uncharged capacitor of capacitance C2 a resistance R. The switch is closed at t = 0. Choose the correct option(s):
The initial current through the resistance is VR
The current through the resistance as a function of time is i(t)=VRe−tτ where τ=R(C1C2C1+C2)
The charge on capacitor C1 as a function of time is q1(t)=(C1VC1+C2)(C1+C2e−tτ)
After a long time, the potential difference across the capacitor C1is(C1C1+C2)V
The correct Answer is:A, B, C, D
After a long time, when the current through the circuit has become zero, the potential difference across the two capacitors is equal (since KVL must be satisfied)
So, q1C1=q2C2 Also, conserving charge q1+q2=C1V.
Solving, we get q1=(C21C1+C−(2))V.
Similar Questions
A capacitor of capacitance 2.0μF is charged to a potential difference of 12 V. It is then connected to an uncharged capacitor of capacitance 4.0μF. Find (a) the charge flow through connecting wire upto study strate on each of the two capacitors after the connection in μC (b) The total electrostatic energy stored in both capacitors in μJ (c) the heat produced during the charge transfer from one capacitor to the other in μJ.
View SolutionA capacitor of capacitance C is charged to a potential difference V0 and then connected with a resistance and a battery of EMF 3V0 such that the positively charged plate of the capacitor is connected to the positive terminal of the battery. The total heat generated in the resistance until the current in the circuit becomes zero is n(CV20). the value of n is ________.
View Solution
Knowledge Check
- Question 1 - Select One
A capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
A12C0V20B13C0V20C16C0V20D18C0V20 - Question 2 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1 - Question 3 - Select One
A capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
AC1VC1+C2BC2VC1+C2C1+C2C1D1−C2C1
A capacitor of capacitance C charged by battery at V volt and then disconnected. At t = 0, it is connected to an uncharged capacitor of capacitance 2C through a resistance R. The charge on the second capacitor as a function of time is given by q=αCV3(1−e−3tβRC) then fing the value of αβ.
View SolutionA capacitor ' "c'" is charged to a potential "difference "V" and then it is connected to an uncharged capacitor of capacitance "'3c'." Now total loss is "(3(β−1)cv2)" .The value of "β" is "]
View SolutionTwo parallel plate capacitor of capacitance 2C and C are charged to the potentials 2 V and V respectively and are connected in a circuit along with a resistance R as shown in the diagram. The switch k is closed at t=0. Find the current in the circuit as a function of time and total heat produced in the circuit
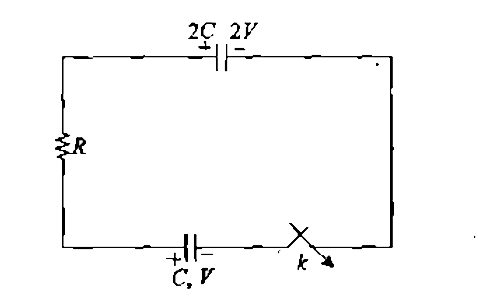View SolutionA capacitor of capacitance C0 is charged to a potential V0 and is connected with another capacitor of capacitance C as Shown . After closing the switch S, the common potential across the two capacitors becomes V . The capacitance C is given by
View SolutionA capacitor C1 of capacitance C is charged to a potential difference V0. The terminal of the charged capacitor are then connected to an uncharged capacitor C2of capacitance C/2. Match the entries of Column I with the entries of Column II and choose the correct option from the codes given below.
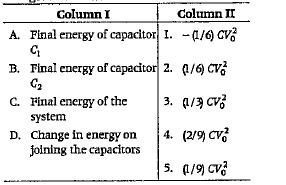View Solution