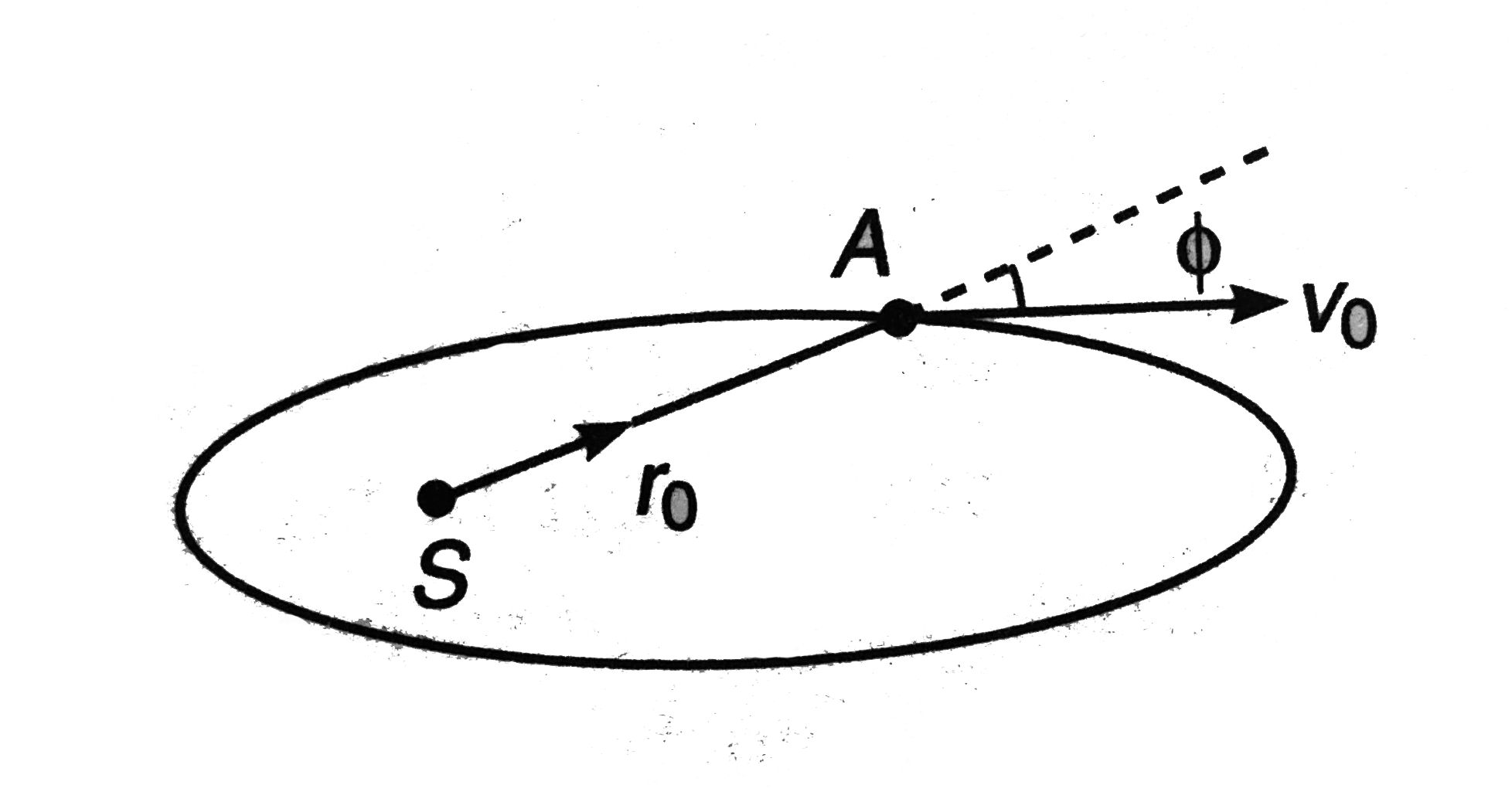
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance $r_{0}$ from the Sun its velocity was equal to $v_{0}$ and the angle between the radius vector $r_{0}$ and the velocity vector $v_{0}$ was equal to $α$ . Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.

Video Solution

Text Solution

Verified by Experts

From the conservation of angular momentum about the Sun.
$m v_{0} r_{0} sin α = m v_{1} r_{1} = m v_{2} r_{2}$ or, $v_{1} r_{1} = v_{2} r_{2} = v_{0} r_{2} sin α$ (1)
From conservation of mechanical energy,
$\frac{1}{2} m v_{0}^{2} - \frac{γ m_{s} m}{r_{0}} = \frac{1}{2} m v_{1}^{2} - \frac{γ m_{s} m}{r_{1}}$
or, $\frac{v_{0}^{2}}{2} - \frac{γ m_{s}}{r_{0}} = \frac{v_{0}^{2} r_{0}^{2} {sin}^{2} α}{2 r_{1}^{2}} - \frac{γ m_{s}}{r_{1}}$ (Using 1)
or, $(v_{0}^{2} - \frac{2 γ m_{s}}{r_{0}}) r_{1}^{2} + 2 γ m_{s} r_{1} - v_{0}^{2} r_{0}^{2} sin α = 0$
So, $r_{1} = \frac{- 2 γ m_{s} \pm \sqrt{4 γ^{2} m_{s}^{2} + 4 (v_{0}^{2} r_{0}^{2} {sin}^{2} α) (v_{0}^{2} - \frac{2 γ m_{s}}{r_{0}})}}{2 (v_{0}^{2} - \frac{2 γ m_{s}}{r_{0}})}$
$= \frac{1 \pm \sqrt{1 - \frac{v_{0}^{2} r_{0}^{2} {sin}^{2} α}{γ m_{s}} (\frac{2}{r_{0}} - \frac{v_{0}^{2}}{r m_{s}})}}{(\frac{2}{r_{0}} - \frac{v_{0}}{γ m_{s}})} = \frac{r_{0} [1 \pm \sqrt{1 - (2 - η) η {sin}^{2} α}]}{(2 - η)}$
where $η = v_{0}^{2} r_{0} / γ m_{s}$ , ( $m_{s}$ is the mass of the Sun).

Updated on:21/07/2023