Find the maximum and minimum distances of the planet A from the sun S, if at a ceration moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
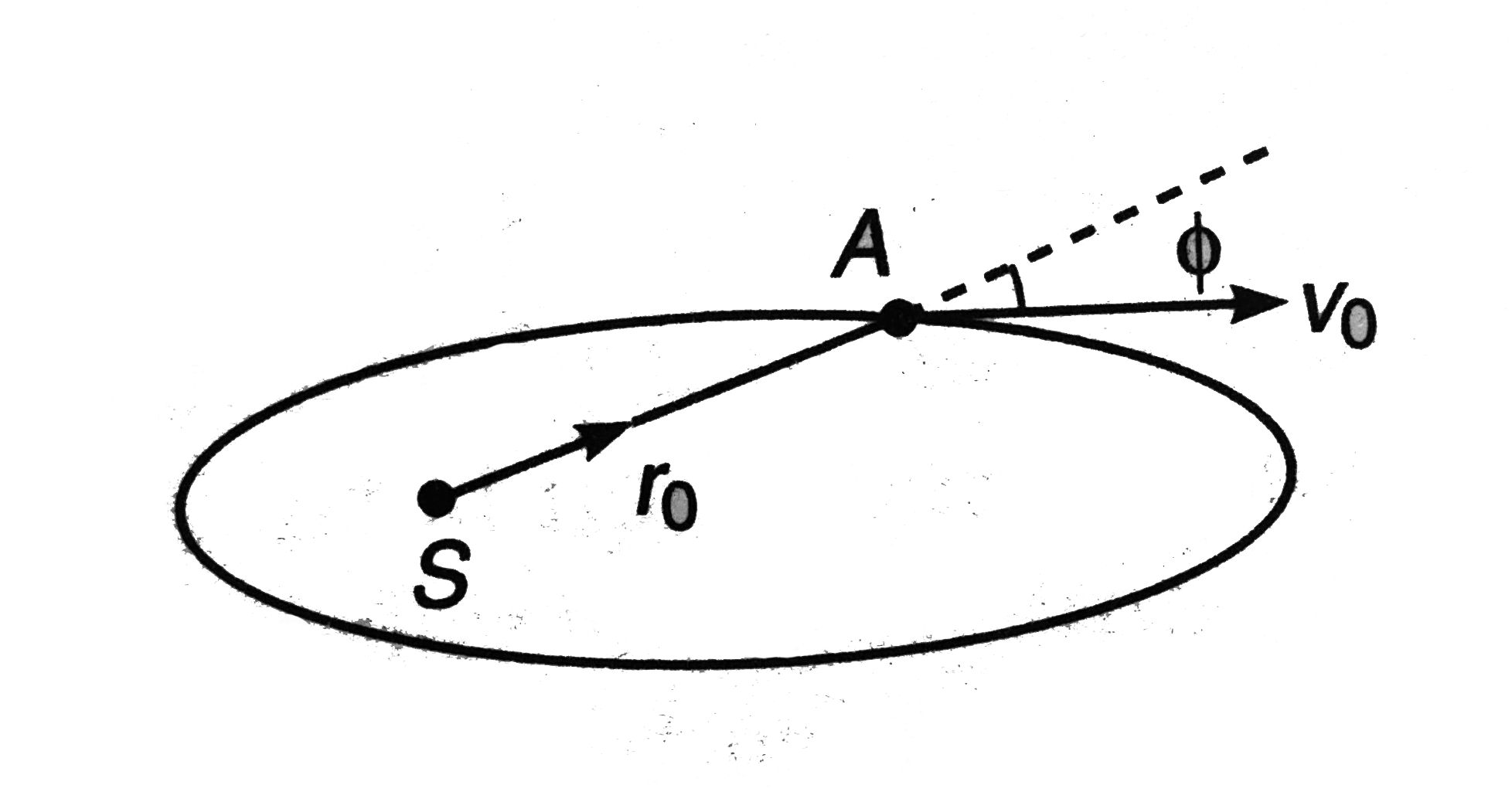
At minimum and maximum distance velocity vector (V) makes an angle of 90∘ with radius vector. Hence, from conservation of angular momentum,
μυ0r0sinϕ=mrυ ..(i)
Hence, m is the mass of the plant.
From energy conservation law, it follows that
mυ202−GMmr0=mυ22−GMmr ..(ii)
Hence, M is the mass of the sun.
Solving Eqs. (i) and (ii) for r, we fet two values of r, one is rmax and another is rmin. So,
rmax=r02−K(1+√1−K(2−K)sin2ϕ)
and rmin=r02−K(1−√1−K(2−K)sin2ϕ)
Here, K=r20υ20GM
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
View SolutionIf the minimum and maximum distance to revolve around the sun is x1 and x2 respectively. Calculate velocity to revolve is v0 then the maximum velocity is
View Solution
Knowledge Check
The ratio of mean distances of three planets from the sun are 0.5:1:1:5, then the square of time periods are in the ratio of
A1:4:9B1:9:4C1:8:27D2:1:3The minimum and maximum distances of a planet revolving around sun are r and R . If the minimum speed of planet of its trajectory is v0 , its maximum speed will be
Av0RrBv0rRCv0R2r2Dv0r2R2The maximum and minimum distances of a comet from the Sun are and 8×1012 and 1.6×1012 If its velocity when nearest to the Sun is 60ms−1 what will be its velocity in ? when it is farthest?
A12B6C112D60
The minimum and maximum distances of a planet revolving around the Sun are x1 and x2. If the minimum speed of the planet on its trajectory is v0 then its maximum speed will be :
View SolutionThe maximum and minimum distances of a comet from the sun are 8×1012m and 1.6×1012m, respectively. If its velocity whien it is nearest to the sun is 60 m / s, then what will be its velocity (in m / s ). when it is farthest from the sun?
View SolutionA planet goes around the sun in an elliptical orbit. The minimum distance of the planet from the Sun is 2×1012m and the maximum speed of the planet in its path is 40kms−1. Find the rate at which its position vector relative to the sun sweeps area, when the planet is at a distance 2.2×1012 from the sun.
View SolutionA particle of mass m moves due to the force F=−αmr, where α is a positve constant ,r is the radius vector of the particle relative to the origin of coordinates. Find the trajectory of its motion if at the initial moment r=r0i and the velocity v=υ0j, whee i and j are the unit vectors of the x and y axes.
View SolutionThe maximum and minimum distance of a comet form the sun are 8×1012mand1.6×1012m. If its velocity when nearest to the sun is 60m/s, what will be its velocity in m/s when it is farthest
View Solution
