Three spherical shells of masses M, 2M and 3M have radii R, 3R and 4R as shows in figure. Find net potential at point P, where CP=2R.
−13GM12R
−23GM6R
zero
−23GM12R
The correct Answer is:D
Pint p lies outside the innermost shall. So, in the denominator we will substitude actual distance of p from the center or r=CP=2R. ltbr gt This point p lies inside the other two shells. So, we substitude their radii, 3r and 4R in the denominator.
∴VP=−GM2R−G(2M)3R−G(3M)4R=−23GM12R
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.1
5 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Three concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
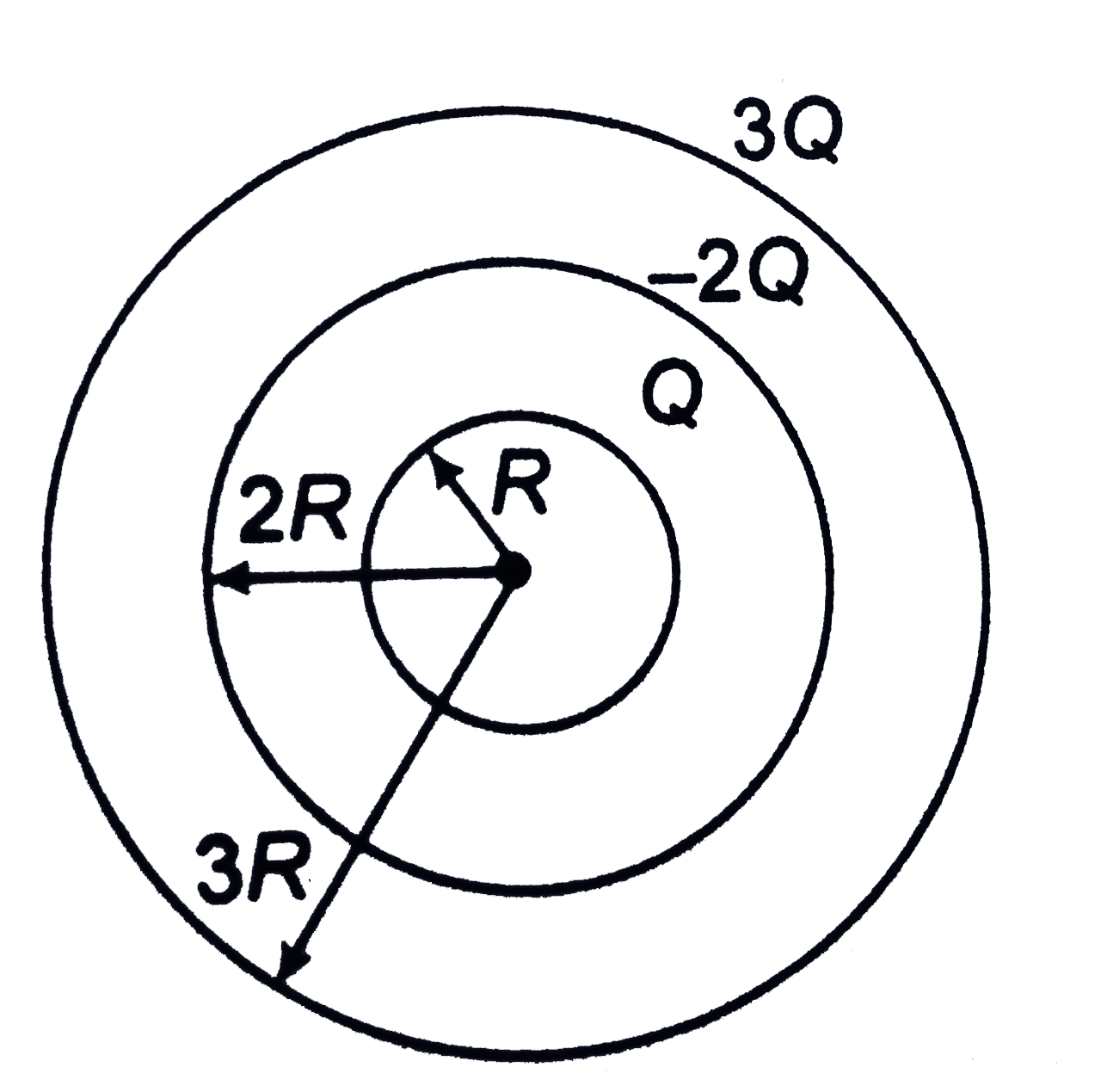
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre. ltbr> b. Compute the electric field at r=52R
c.computethe→tale≤ctrostatice≠rgys→red∈thesystem.<br>The∈≠rshellisnowco∩ected→theexternalo≠byaconduct∈gwire,passingthroughaverysmallho≤∈them≤shell.<br>Computethechar≥sonthespheresofradiiRand3R.<br>e.Computethee≤ctricfieldatr=5/2R.
View Solutiona solid sphere of mass m and radius r is plced nside as hollow thin spherical shell of mass and M and radius R as shown in figure. A particle of mas m is placed on tehline joining the tow centres ast a distance x from the point of contct of th sphere and teh shell. Findn teh mgnitude fo the resultant gravitational force on this particle due to the sphere and the shell if a. r<x<2r,b.2r<x<2Randc.x>2R.
View Solution
Knowledge Check
Three spherical shells of masses M, 2M and 3M have radii R, 3R and 4R as shows in figure. Find net potential at point P, where CP=2R.
A−13GM12RB−23GM6RCzeroD−23GM12RTwo concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure
If we draw a graph between potential V and distance r from the centre, the graph will be likeA
B
C
D
Consider a thin spherical shell of uniform density of mass M and radius R:
AThe gravitational field inside the shell will be zeroBThe gravitational self energy of shell is GM22RCAttractive force experience by unit area of the shell pull the other half is GM22R2DNet gravitational force with which one hemisphere of the shell arracts other, is GM28R2
Two concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
View SolutionTwo concentric spherical shells A and B of radii R and 2R and mases 4M, and M, respectively are placed in space as shown in Fig. The gravitational potential at P at a distance r(R<r<2R)from the centre of shells is
View SolutionA point charge q is placed inside a conducting spherical shell of inner radius 2R and outer radius 3R at a distance of R from the center of the shell. Find the electric potential at the center of the shell.
View Solution