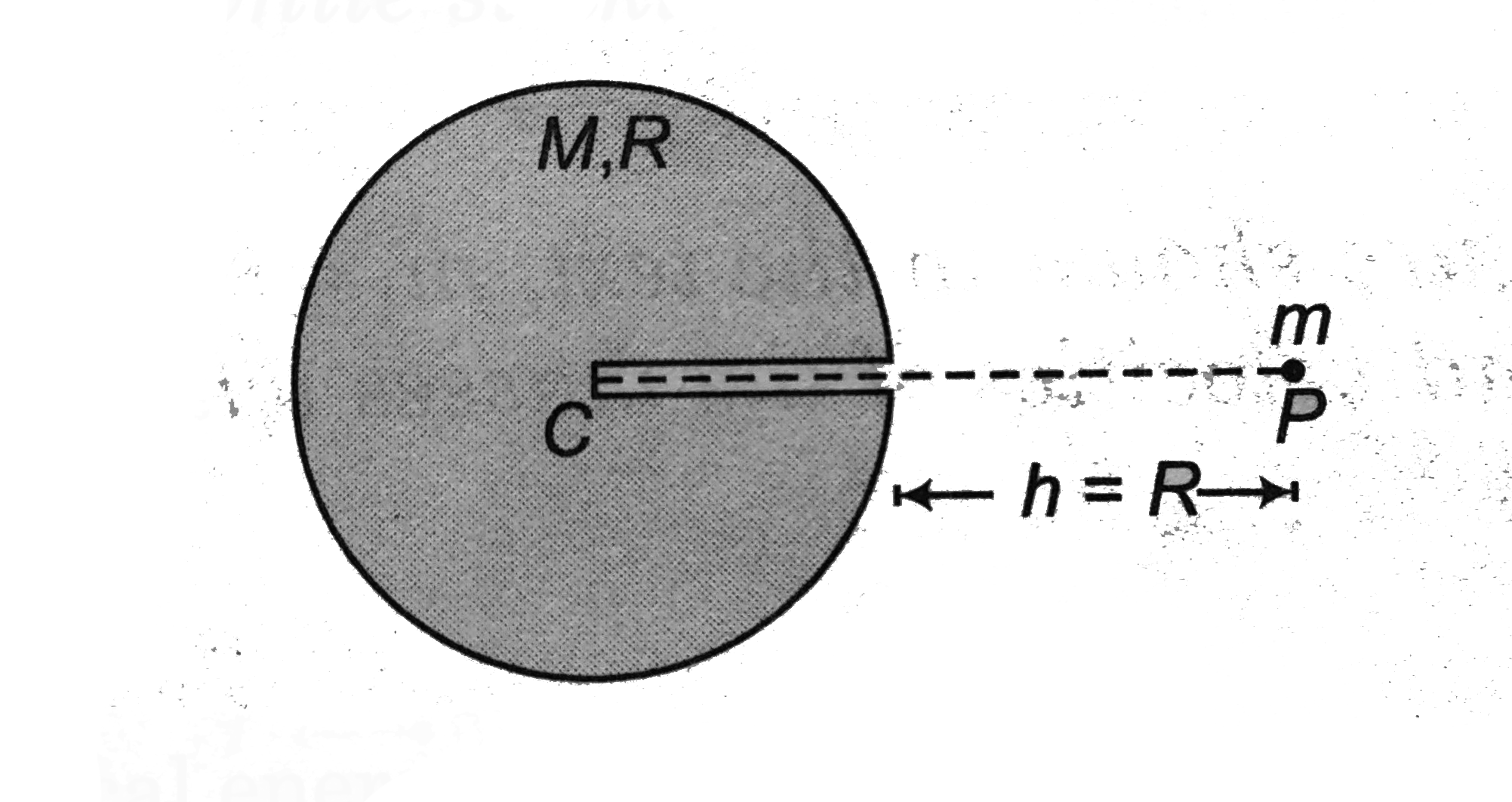
There is a smooth tunnel upto centre C of a solid sphere of mass 'M' and radius R.A particle of mass m(<<M) is realeased from point P along the line CP. Find velocity of 'm' while striking at C.
.
The correct Answer is:B, C
Using mechanical energy conservation equation.
EC=EP⇒KC+UC=KP+UP
⇒12mυ2C+mVC=0−GMm(R+R) ..(i)
Here, VC= potential at C due to mass M=−32GMR
Substituting this value in Eq. (i) and then solving we get,
υC=√2GMR
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples8videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Exercise 13.15videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
Similar Questions
From a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in figure−6.30. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this - particle due to the sphere and the shell if (a) r<x<2r,(b)2r<x<2Rand(c)x>2R.
View Solution
Knowledge Check
- Question 1 - Select One
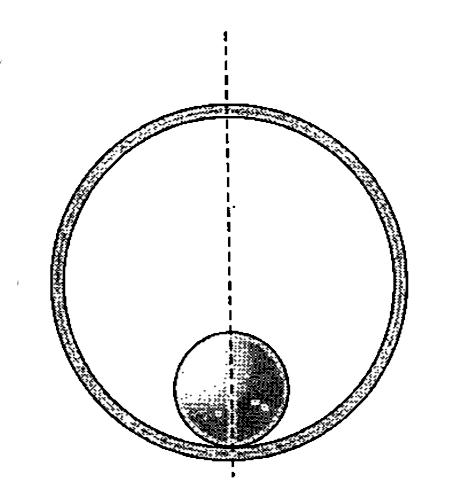
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.
What time will it take to move from A to B?A=R2√GMhB>R2√GMhC<R2√GMhDNone of these - Question 2 - Select One
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.
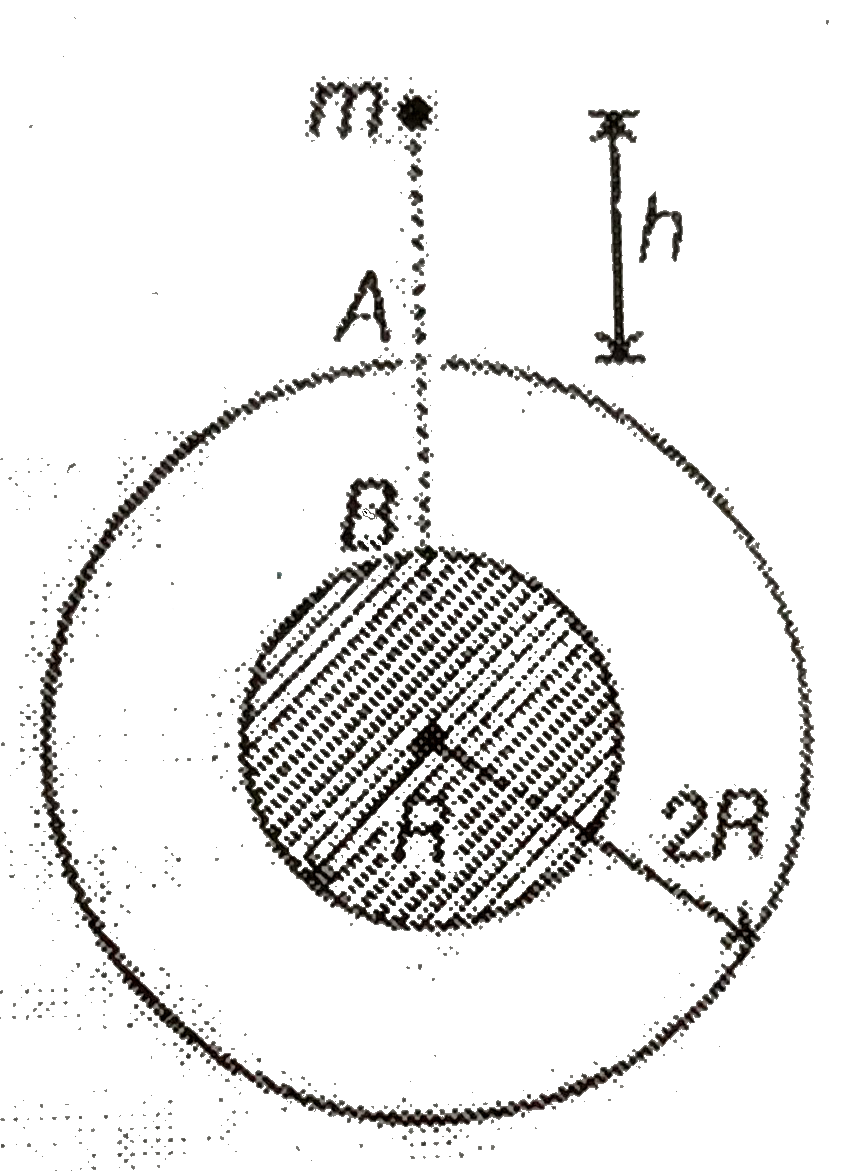
What speed will it collide at B?A√2GMRB√GM2RC√3GM2RD√GMR - Question 3 - Select One
_S01_036_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass and radius 2R as shown. A small particle of mass m is relased from rest from a height h(<<R) above the shell. There is a hole in the shell.
Q. In what time will it enter the hole at AA2√hR2GMB√2hR2GMC√hR2GMDNone of these
A particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
r<x<2rView Solution_E01_070_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole inn the shell.
QWhat time will it take to move from A to B?View Solution_E01_069_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole inn the shell.
QIn what time will it enter the hole at AView SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
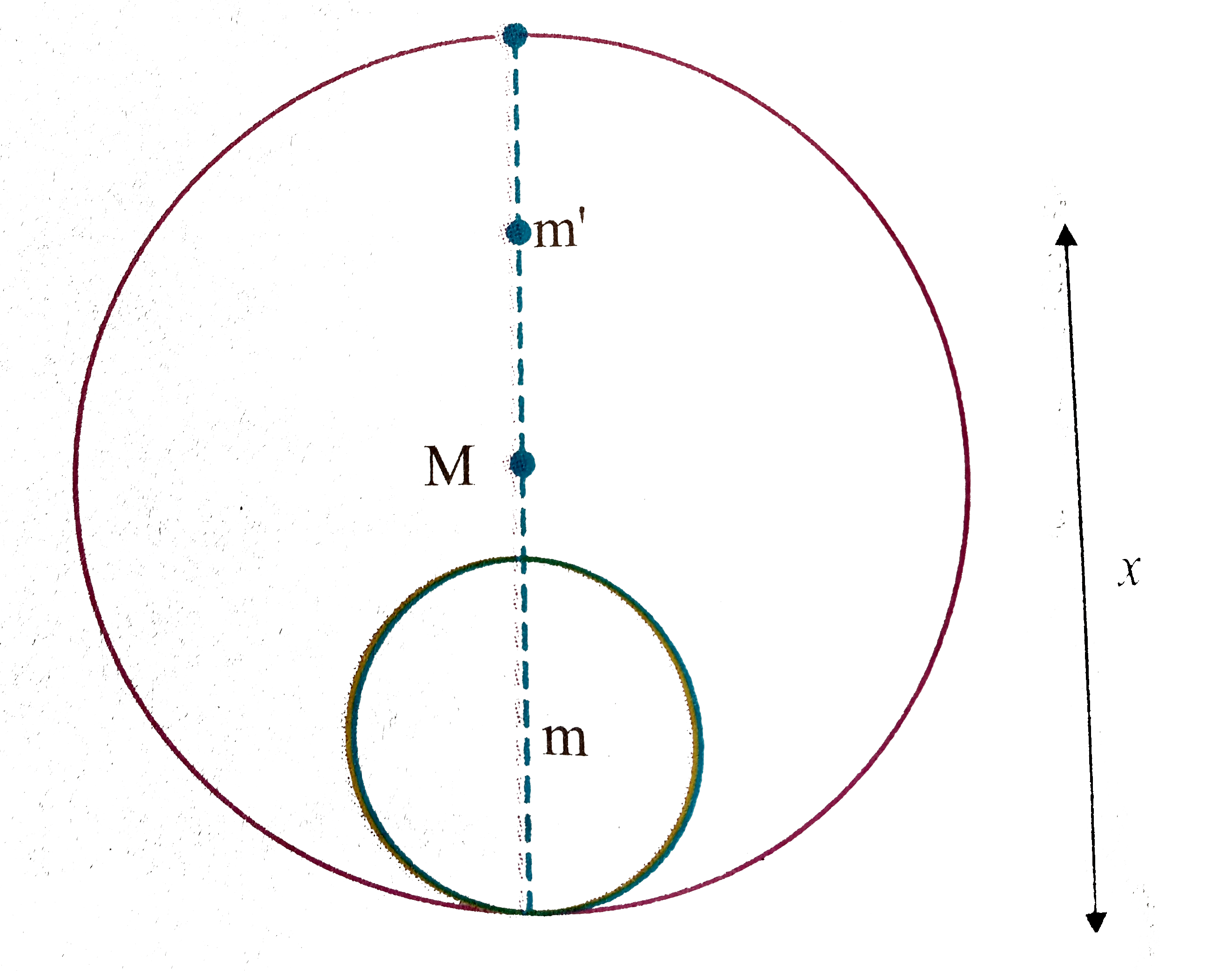
2r<x<2RView Solution