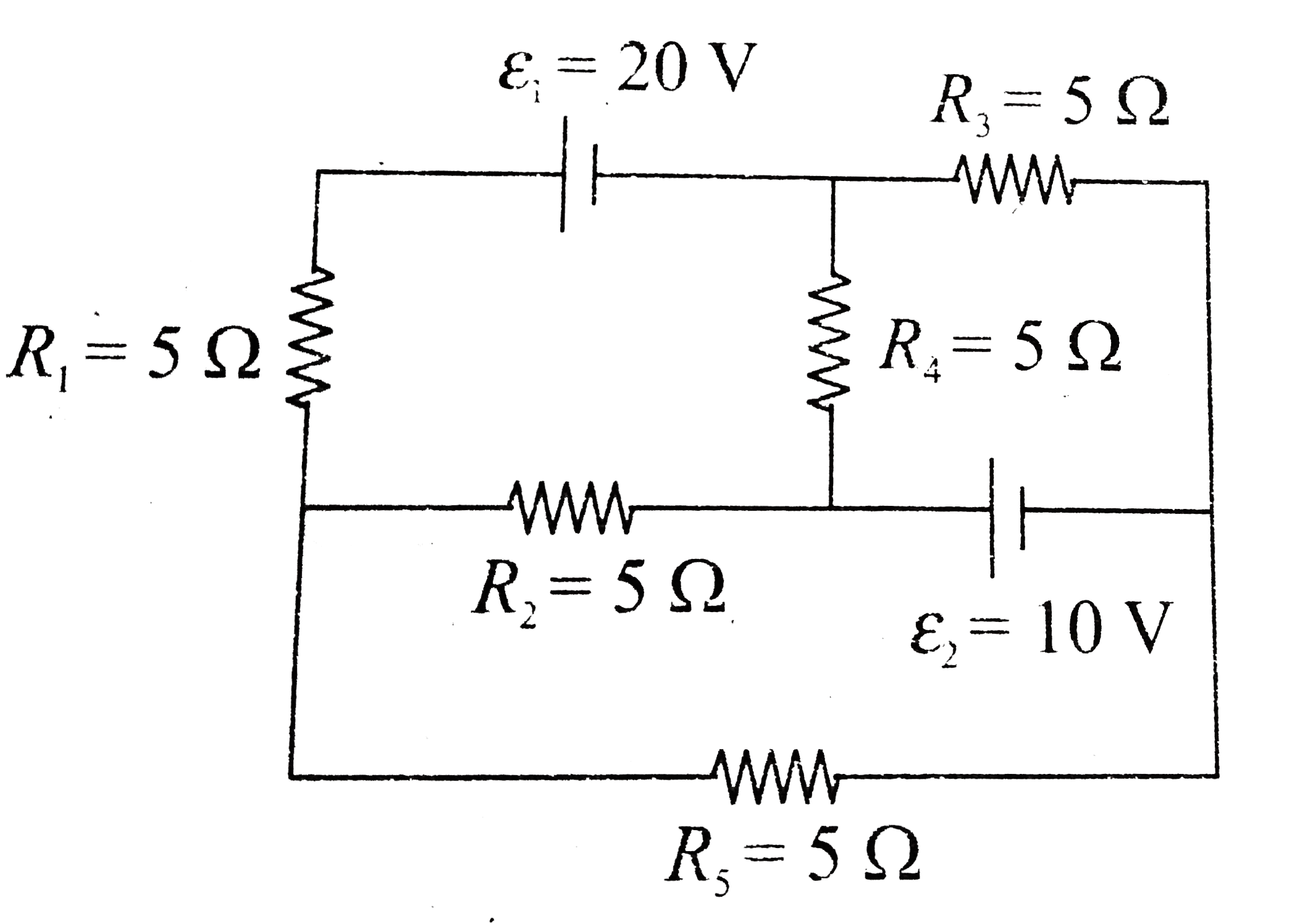
A parallel combination of two cells of emfs ε1 and ε2, and internal resistance r1 and r2 is used to supply current to a load of resistance R. Write the expression for the current through the load in terms of ε1,ε2,r1 and r2.
Equivalent resistance of two cells in parallel
req=r1r2r1+r2
Equivalent emf of two cells in parallel
req=ε1r1+ε2r1r1+r2
Current in circuit,
I=εeqR+req=ε1r2+ε2r1r1+r2R+r1r2(r1+r2)=ε1r2+ε2r1R(r1+r2)+r1r2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Knowledge Check
Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
AThe effective emf of this parallel combination is (ε1r1+ε2r2)(r1+r2)BThe effective internal resistance of this combination is 2r1r2(r1+r2)Cthe effective emf of this parallel combination is (ε1r2+ε2r1)(r1+r2)DThe effective internal resistance of this combination is r1r2(r1+r2)Two batteries of emf ε1 and ε2(ε2>ε1 and internal resistances r1 and r2 respectively are connected in parallel as shown in Fig. 2 (EP).1.
 AThe equivalent emf εeq of the two cells is between ε1 and ε2,i.e.,ε1<εeq<ε2BThe quivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 alwaysDεeq is independent of internal resistances r1 and r2
AThe equivalent emf εeq of the two cells is between ε1 and ε2,i.e.,ε1<εeq<ε2BThe quivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 alwaysDεeq is independent of internal resistances r1 and r24 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
A2AB1.5AC1AD0.888A
Two cells of emf E1andE2 having internal resistance r1andr2 are connected in parallel. Calculate Eeq and req for the combination.
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionA cell of emf ε and internal resistance r is charged by a current I, then
View SolutionThree batteries of emf E1,E2 and E3 and internal resistance r1,r2 and r3 are connected as shown. The current through the battery of emf E3 is zero if.
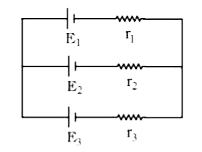
View Solution