A cell of emf $ε$ and internal resistance r is charged by a current I, then

A

the cell stores chemical energy at the rate of $ε i$

B

the cell stores chemical energy at the rate of $i^{2} r$

C

the cell stores chemical energy at the rate of $ε I - i^{2} r$

D

the storage of chemical energy rate cannot be calculated

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

c. From work-energy theorem, we get $Δ = ε i - i^{2} r$ .

|

Updated on:21/07/2023

Class 12 PHYSICS CURRENT ELECTRICITY

Similar Questions

Knowledge Check

Question 1 - Select One
A cell of emf $ε$ and internal resistance $r$ drives a current $i$ through an extermal resistance $R$
(i) The cell suppllied $ε i$ power
(ii) Heat is produced in $R$ at the rate $ε i$
(iii) Heat is produced in $R$ at the rate $ε I (\frac{R}{R + r})$
(iv) Heat is produced in the cell at the rate $ε i ((r \frac{?}{R + r})$
A(i) , (ii)
B(ii), (iii)
C(i),(iii),(iv)
Dall
Question 2 - Select One
A student measures the terminal potential difference $(V)$ of a cell (of emf $ε$ and internal resistance $r$ ) as a function of the current $(I)$ flowing through it. The slope and intercept of the graph between $V$ and $I$ , then respectively, equal
A $ε$ and $- r$
B $- r$ and $ε$
C $r$ and $- ε$
D $- ε$ and $r$
Question 3 - Select One
An accumulator battery (storage cell) $B$ of emf $ε$ and internal resistance $r$ is being charged from $D C$ supply whose terminals are $T_{1}$ and $T_{2}$
.
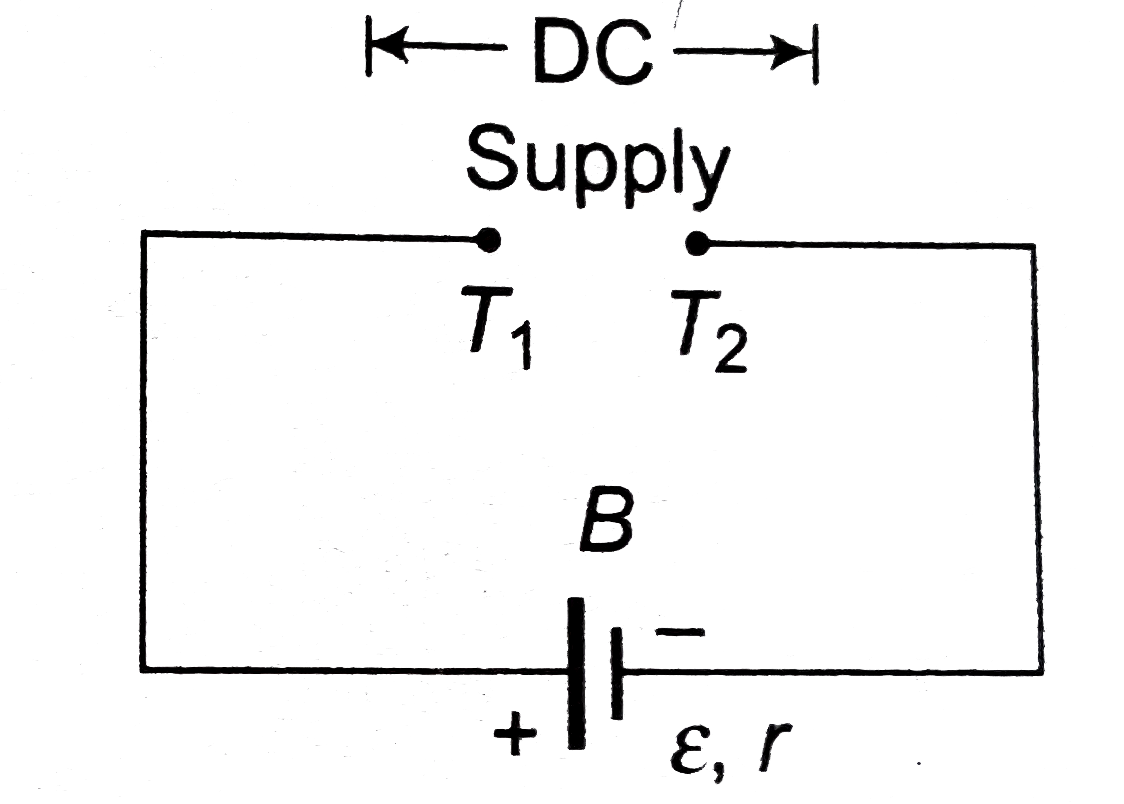APotential difference between $T_{1}$ and $T_{2}$ must be $> ε$
B $T_{1}$ must be positive with respect to $T_{2}$
CIn the battery, current flows from the positive to the negative terminal
DAll the above options are correct.

Recommended Questions

Home
Ask Doubt
Profile