Two cells of emfs $ε_{1} and ε_{2}$ and internal resistances $r_{1} and r_{2}$ respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.

Video Solution

Text Solution

Verified by Experts

According to Kirchhoff first law ,

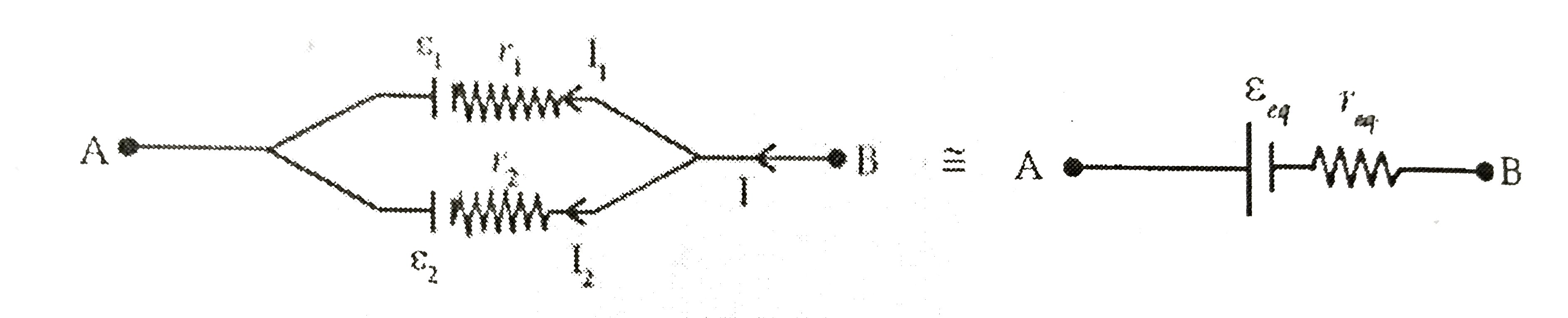
$I = I_{1} + I_{2}$ . . . (i)
Potential across upper branch $V = ε_{1} - I_{1} r_{1}$ . . . (ii)
Potential across lower branch $V = ε_{2} - I_{2} r_{2}$ . . . (iii)
Potential across equivalent branch $V = ε_{e q} - I_{req}$ . . . (iv)
Substituting the values of I , $I_{1} and I_{2}$ from equations (ii) , (iii) and (iv) in equation (i),
$\begin{matrix} \frac{ε_{e q}}{r_{e q}} - \frac{V}{r_{e q}} = \frac{ε_{1}}{r_{1}} - \frac{V}{r_{1}} + \frac{ε_{2}}{r^{2}} - \frac{V}{r_{2}} & \frac{ε_{e q}}{r_{e q}} - \frac{V}{r_{e q}} = \frac{ε_{1}}{r_{1}} + \frac{ε_{2}}{r_{2}} + (\frac{1}{r_{e q}} + \frac{1}{r_{e q}}) V \end{matrix}$
Comparing both the sides , $\frac{ε_{e q}}{r_{e q}} = \frac{ε_{1}}{r_{1}} + \frac{ε_{2}}{r_{2}} and \frac{1}{r_{e q}} = \frac{1}{r_{1}} + \frac{1}{r_{2}}$

Updated on:21/07/2023

Two batteris of emf $ε_{1}$ and $ε_{2}$ wit respective internal resistance $r_{1}$ and $r_{2}$ are connected in parallel. Now
AThe effective emf of this parallel combination is $\frac{(ε_{1} r_{1} + ε_{2} r_{2})}{(r_{1} + r_{2})}$
BThe effective internal resistance of this combination is $\frac{2 r_{1} r_{2}}{(r_{1} + r_{2})}$
Cthe effective emf of this parallel combination is $\frac{(ε_{1} r_{2} + ε_{2} r_{1})}{(r_{1} + r_{2})}$
DThe effective internal resistance of this combination is $\frac{r_{1} r_{2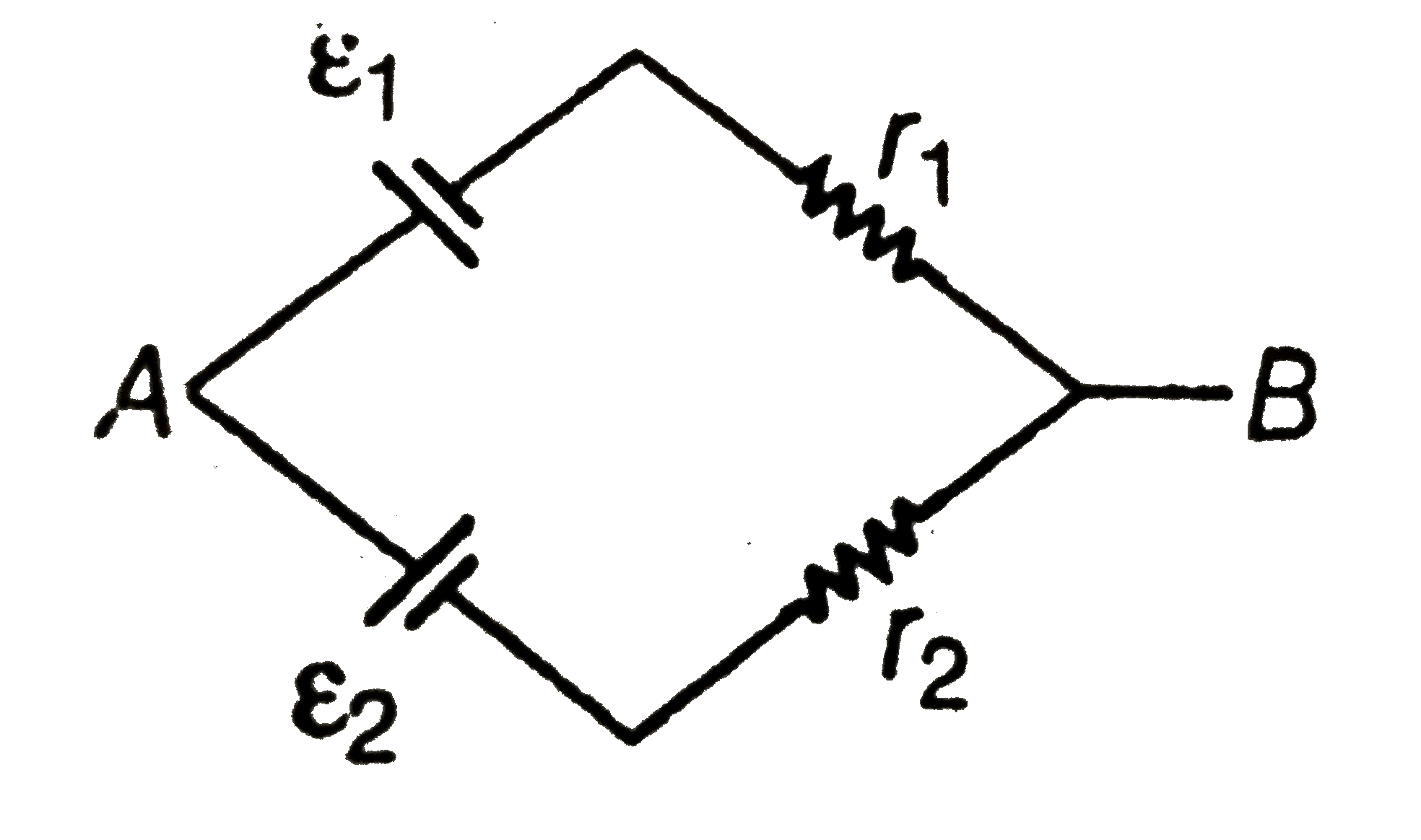}}{(r_{1} + r_{2})}$
Two batteries of emf $ε_{1} and ε_{2} (ε_{2} > ε_{1})$ and internal resistance $r_{1} and r_{2}$ respectively are connected in parallel as shown in figure.
AThe equivalent emf $ε_{e q}$ of the two cells is between $ε_{1} and ε_{2}$ , i.e., $ε_{1} < ε_{e q} < ε_{2}$
Bthe equivalent emf $ε_{e q}$ is smaller than $ε_{1}$
CThe $ε_{e q}$ is given by $ε_{e q} = ε_{1} + ε_{2}$ always.
D $ε_{e q}$ is independent of internal resistance $r_{1} and r_{2}$ .
Two batteries of emf $ε_{1}$ and $ε_{2} (ε_{2} > ε_{1}$ and internal resistances $r_{1}$ and $r_{2}$ respectively are connected in parallel as shown in Fig. 2 (EP).1.

AThe equivalent emf $ε_{e q}$ of the two cells is between $ε_{1}$ and $ε_{2}, i . e ., ε_{1} < ε_{e q} < ε_{2}$
BThe quivalent emf $ε_{e q}$ is smaller than $ε_{1}$
CThe $ε_{e q}$ is given by $ε_{e q} = ε_{1} + ε_{2}$ always
D $ε_{e q}$ is independent of internal resistances $r_{1}$ and $r_{2}$