Two cells of emf E each and internal resistance $r_{1}$ and $r_{2}$ are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between $R, r_{1}$ and $r_{2}$

Video Solution

Text Solution

Verified by Experts

Current l from positive electrons of both are equal.
$I = \frac{E_{e q}}{R + r_{e q}} = \frac{2 E}{R + (r_{1} + r_{2})}$
Potential difference across first cell $= V_{A} - V_{B} = 0$
$\Rightarrow E - l r_{1} = 0$
$\Rightarrow E - \frac{2 E}{R + (r_{1} + r_{2})} r_{1} = 0$
$\Rightarrow R + r_{1} + r_{2} - 2 r_{1} = 0$
$\Rightarrow R + r_{2} - r_{1} = 0$
$\Rightarrow r_{1} = R + r_{2} = R = (r_{1} - r_{2})$

Updated on:21/07/2023

Two cells of emf 3V and 5V and internal resistance $r_{1}$ and $r_{2}$ respectively are in series with an external resistance R. if the p.d. across 1 st cell is zero, then R is
A $\frac{5 r_{1} - 3 r_{2}}{3}$
B $\frac{2 r_{1} - 3 r_{2}}{4}$
C $\frac{3 r_{1} - 5 r_{2}}{3}$
D $\frac{4 r_{1} - 5 r_{2}}{3}$
Two sources of emf $6 V$ and internal resistance $3 Ω$ and $2 Ω$ are connected to anexternal resistance $R$ as shown. If potential difference across battery $A$ is zero, then the value of $R$ ( in $Ω$ ) is

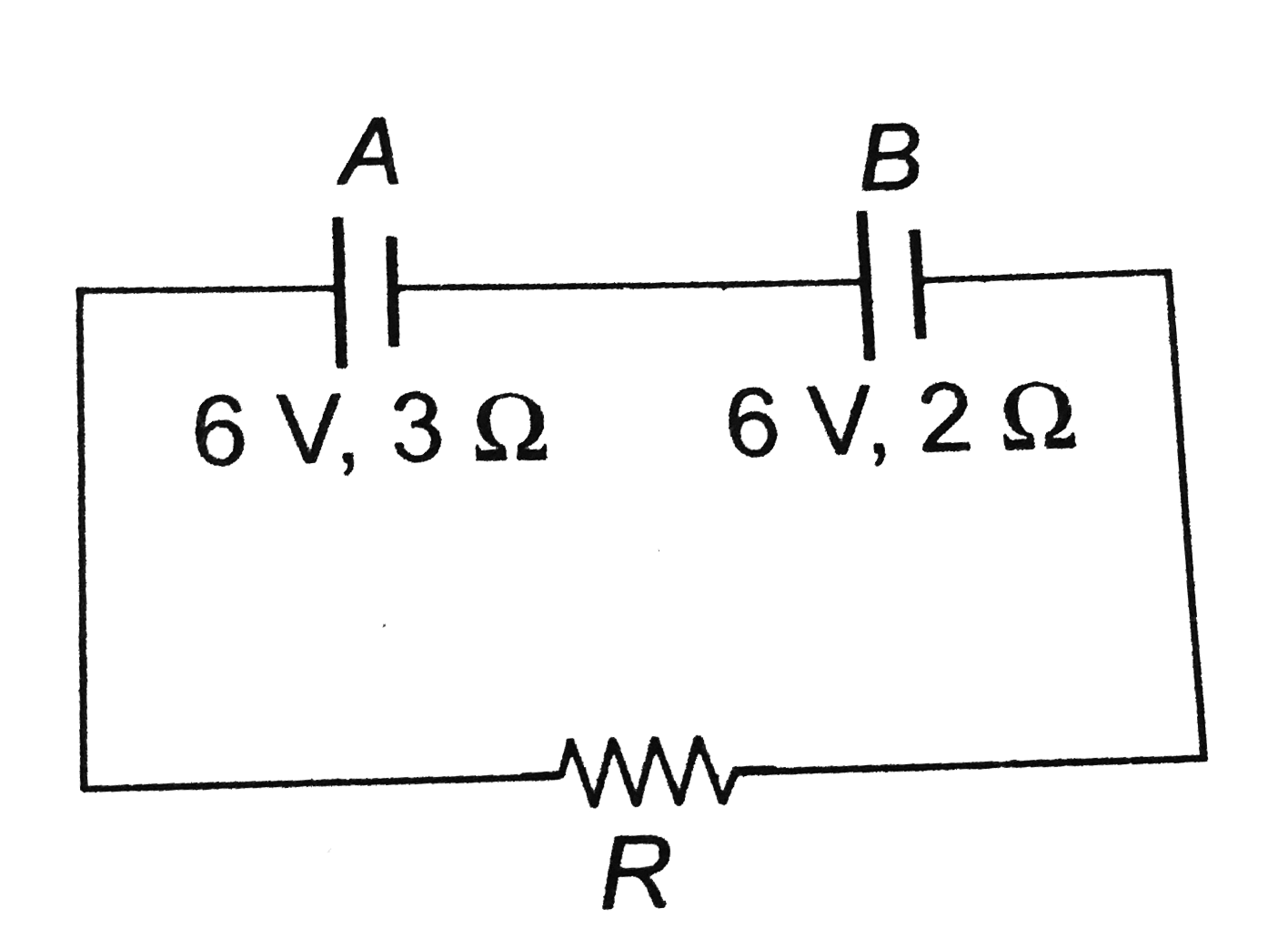A $1 Ω$
B $2 Ω$
C $3 Ω$
D $4 Ω$
Two cells of the same e.mf. e but different internal resistances $r_{1} and r_{2}$ are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

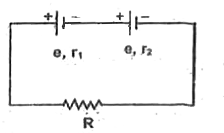A $r_{1} - r_{2}$
B $\frac{r_{1}}{r_{2}}$
C $r_{1} r_{2}$
D $r_{1} + r_{2}$