Two cells each of emf E and internal resistacne r1 and r2 respectively are conneted in series with an external resistance R. The potential defference between the terminats of the first cell will be zero when R equal to
r1+r22
√r21r21
r1−r2
r1r2r1+r2
The correct Answer is:C
Step by step video, text & image solution for Two cells each of emf E and internal resistacne r_(1)" and "r_(2) respectively are conneted in series with an external resistance R. The potential defference between the terminats of the first cell will be zero when R equal to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-2)
16 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-3)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-3)
2 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
A circuit consists of two cells, each of e.m.f. E and internal resistances r1 and r2 are connected in series through an external resistance X. If the potential difference between the ends of the first cell is zero, the value of X in terms of r1 and r2 will be
View SolutionTwo cells of emf 2E and E with internal resistance r1 and r2 respectively are connected in series to an external resistor R (see figure). The value of R, at which the potential difference across the terminals of the first cell becomes zero is
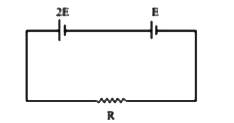
View Solution
Knowledge Check
Two cells of emf 3V and 5V and internal resistance r1 and r2 respectively are in series with an external resistance R. if the p.d. across 1 st cell is zero, then R is
A5r1−3r23B2r1−3r24C3r1−5r23D4r1−5r23Tow cells with the same emf E and different internal resistances r1 and r2 are connected in series to an external resistances R . The value of R so that the potential difference across the first cell be zero is
A√r1r2Br1+r2Cr1−r2Dr1+r22A cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
A(1n)B1(n+1)Cn(n+1)D(n+1)n
Two cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View Solution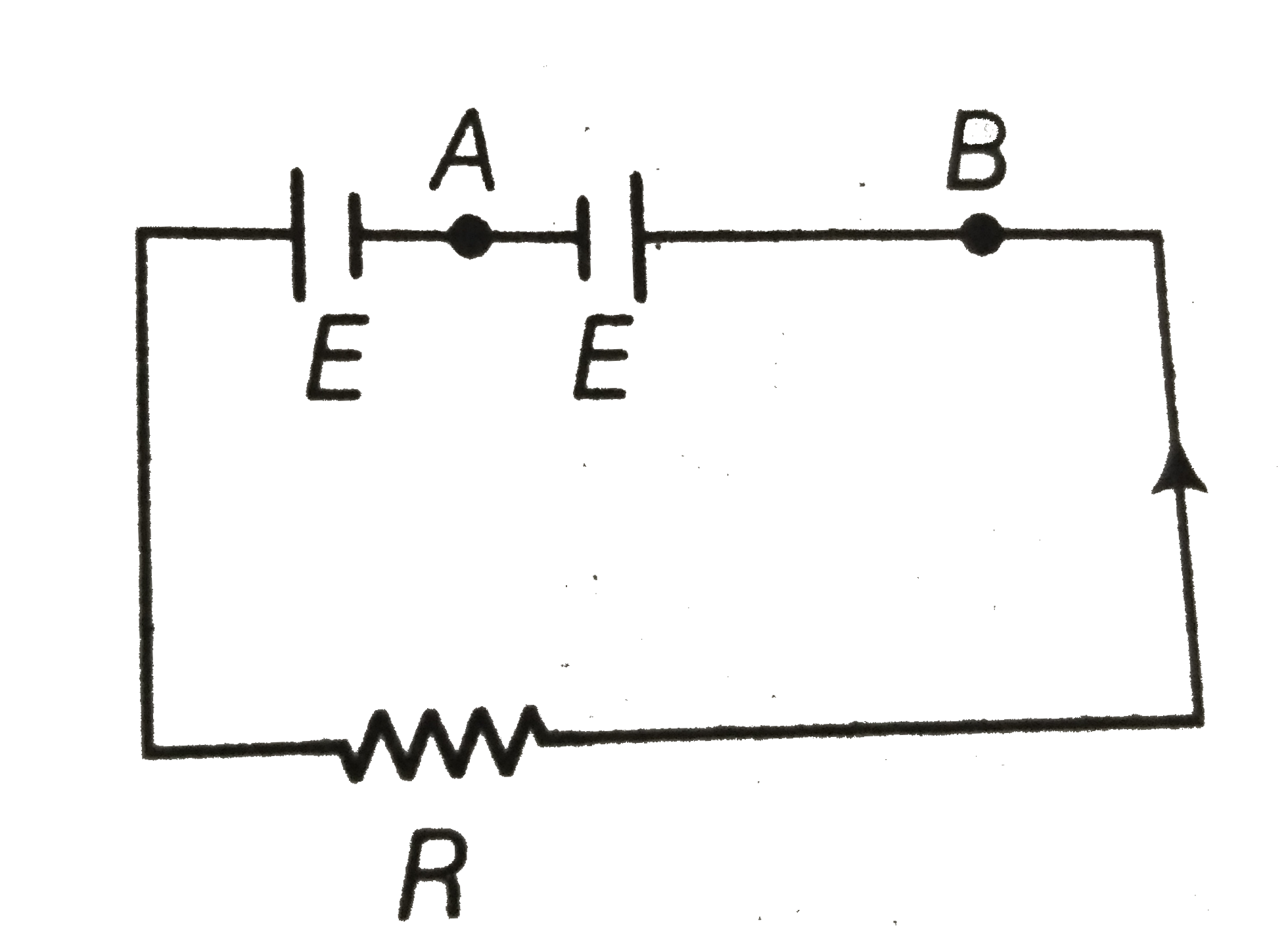
Two cells of same emf E but internal resistance r1andr2 are connected in series to an external resistor R(figure). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero?
View SolutionA cell of emf ε and internal resistance (r) is connected in series with an external resistance (nr) then the ratio of the terminal potential difference to emf is:
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionA cell of e.mf. E and internal resistance r is connected in series with an external resistance nr. Then, the ratio of the terminal potential difference to E.M.F.is
View Solution
