A small mass and a thin uniform rod each of mass 'm' are positioned along the same straight line as shown. Find the force of gravitational attraction exerted by the rod on the small mass.
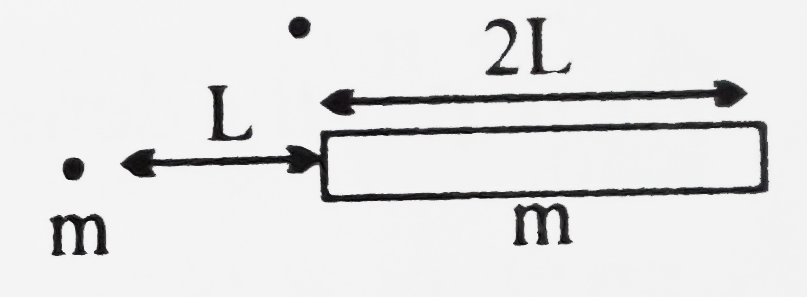
The correct Answer is:Gm23L2
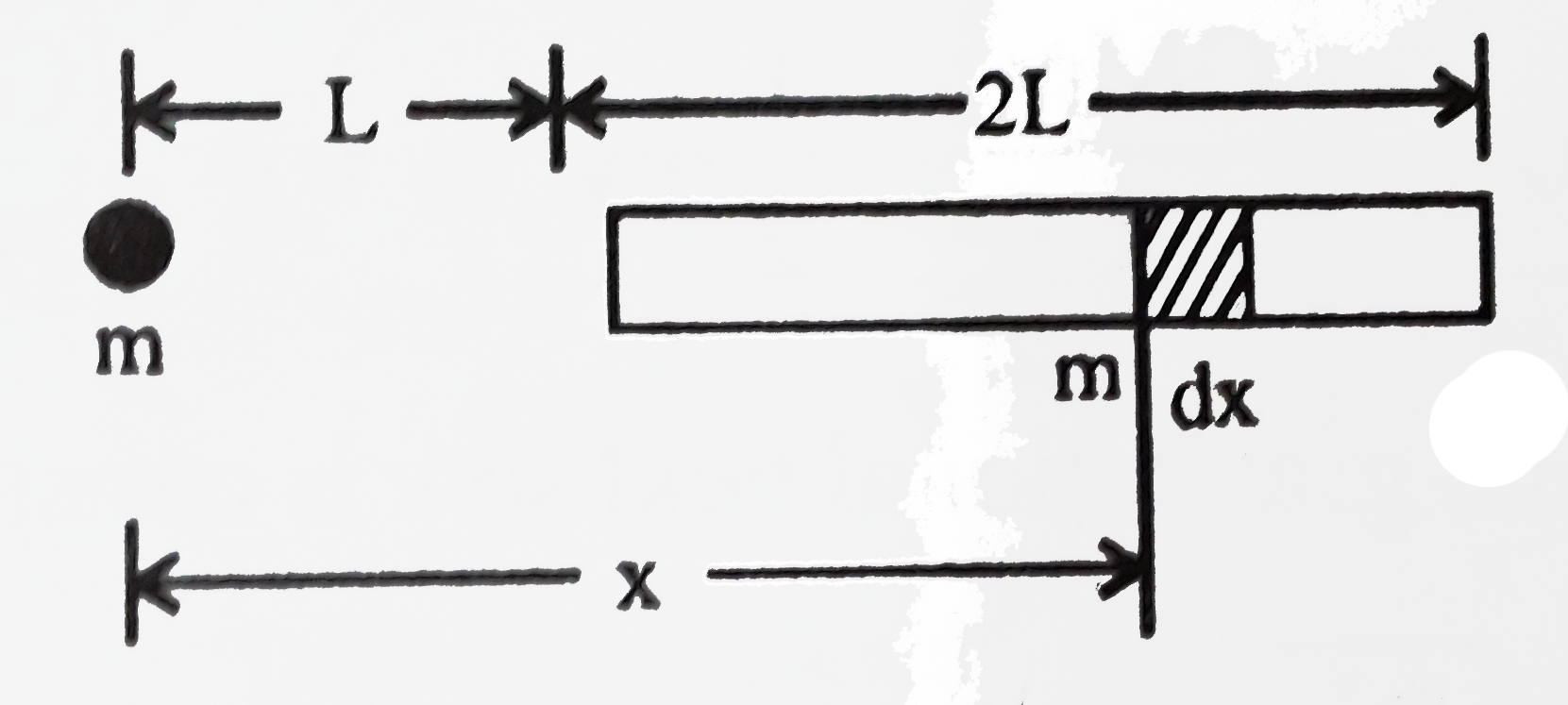
dF=Gmdmx2⇒dF=Gm×m2Ldxx2
df=Gm22Ldxx2
F=∫3LL∫Gm22Ldxx2⇒F=Gm22L[−1x]3LL
F=Gm22L×23L⇒F=Gm23L2
Similar Questions
Knowledge Check
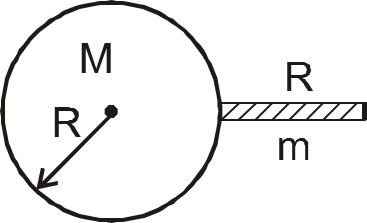
A uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is
 AGMm2R2BGMm4R2C4GMm9R2DGMm8R2
AGMm2R2BGMm4R2C4GMm9R2DGMm8R2A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Find the potential energy of the gravitational interation of a point mass of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line such that the point mass is at a distance 'a' from one end. Also find the force of their interaction.
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is
View SolutionFind the potential energy of the gravitational interaction
(a) of two mass points of masses m1 and m2 located at a distance r from each other,
(b) of a mass point of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line at a distance a from each other, also find the force of their interaction.
View SolutionA uniform rod of mass m and length l is struck at an end by a force F perpendicular to the rod for a short time interval t. Calculate
the speed of the centre of mass,
View SolutionTwo uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View Solution