Two light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The period of SHM of the bead is
2π√3m8K
2π√m3K
3π√2mK
None of these
The correct Answer is:A
Step by step video, text & image solution for Two light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly. The period of SHM of the bead is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Two light vertical springs 1 and 2 of stifiness k and 2k are connected to a light horizontal rod at its two ends as shown. A bead of chewing gam of mass 'm' is sticked gently at the mid point of the rod and lowcred slowly, such that where equilibrium is reached the bead displaced by x0. The period of SHM of the bead is 2π√pnqK, Find |p−q|.
'(##CEN_KSR_PHY_JEE_C16_E01_032_Q16##)'
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
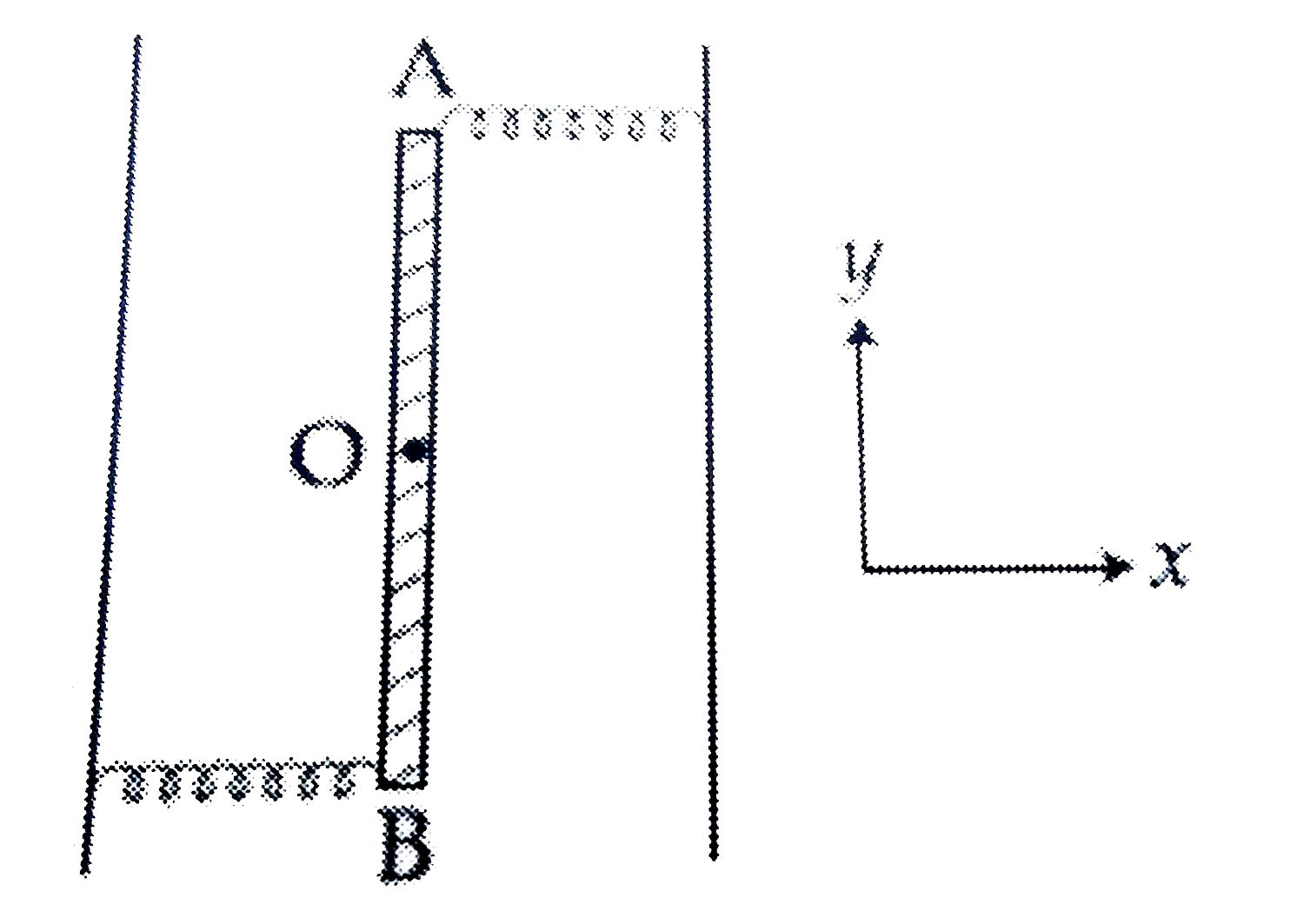
View Solution
Knowledge Check
Two light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The energy of oscillation of the bead for an amplitude y0 is equal to (x0=maximum displacement of the bead in the process of lowering)Amgx0Bmg(x0+y0)C32Ky20D43Ky20Two light verticle springs 1 and 2 of stiffness K and 2K are connected by a 1 light horizontal rod. A bead of chewing gum of mass 'm' is placed gently at the mid point of the rod and lowered slowly.
The ratio of magnitude of work done by the external agent to that by gravity in lowering the bead till it remains at rest isA1:1B1:2C2:1D1:4Two spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
 A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
A(12π)√(Km)B(12π)√(2Km)C(12π)√(3Km)D(12π)√(mK)
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View SolutionA square hinged -structure (ABCD) is formed with four massless rods which lie on the smooth horizontal table. The hinge−D of structure is fixed with table and hinge A, hinge −B and hinge-C are free to move on the table. A point mass m is attached at hinge −B, and an ideal spring of stiffness k is connected between hinge −A and hinge-C as shown in the figure. System is in equilibrium. The mass m is slightly along line BD and released to perform SHM. The time period of SHM is π√nmk. Find

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionA plank of mass M is placed on a smooth hroizonal surface. Two light identical springs each of stiffness k are rigidly connected to structs at the ends of the plank as shown. When the spring are in their unextended position the distance between their free ends is 3l. a block of mass m is placed on the plank and pressed aganist one of the springs so that it is compressed by l. To keep the blocks at rest it is connected to the strut by means of a light string, initially the syetem is at rest. Now the string is burnt.
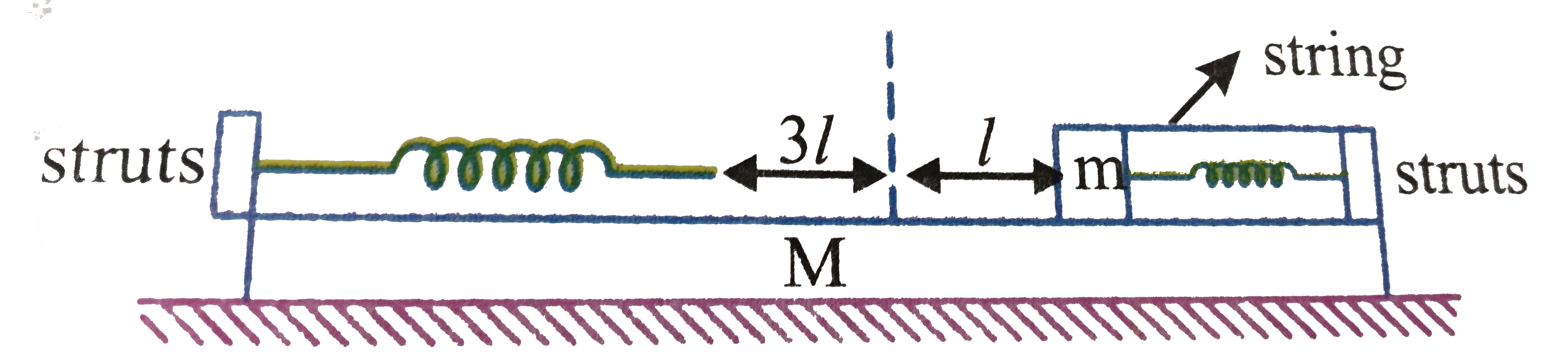
Time period of oscillation of block:
View Solution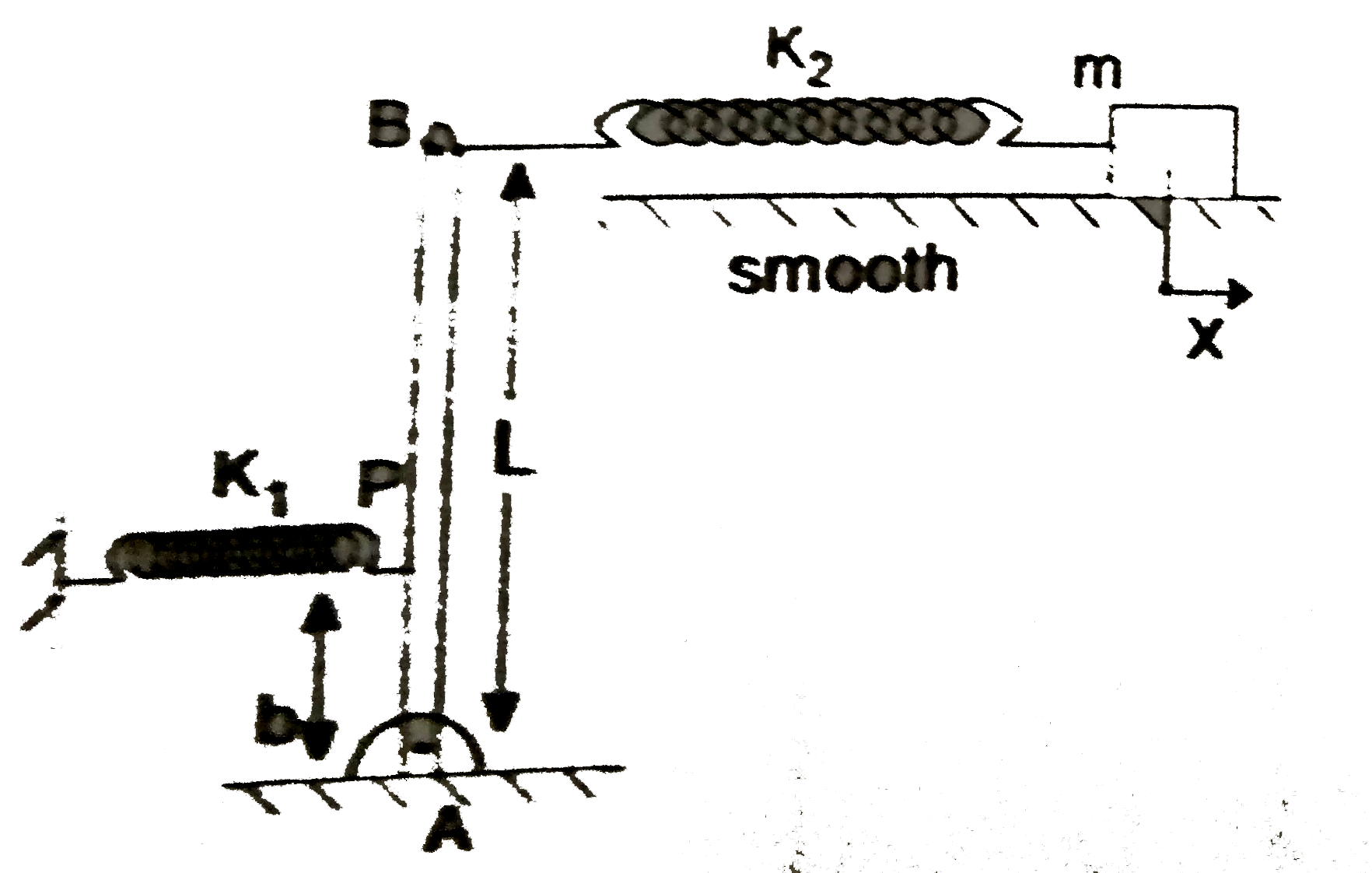
A massless Rod AB is hinged at point A. At point P, it is connected by a spring of stiffness K1 and at point B it is connected to another spring of stiffness K2 connected to mass m as shown in figure the length of Rod AB is l and displaced by a distance x from its mean position as shown in figure then the time period of S.H.M. of mass is
View Solution