AB is a light rigid rod. Which is rotating about a vertical axis passing through A,A spring of force constant K and natural length l is attached at A and its other end is attached to a small bead of mass m. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
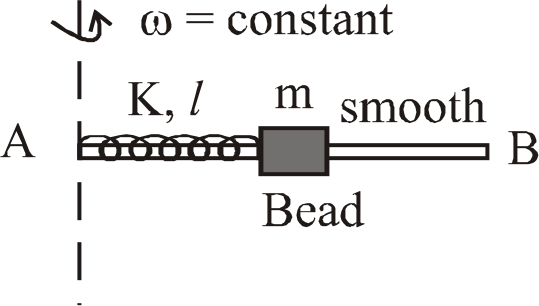
The maximum velocity attained by the bead w.r.t the rod is given by Vmax=√mω4l2K−mω2
The maximum velocity attained by the bead w.r.t the rod is given by Vmax=√(mω4+Kmω2−K)ω2l2
The maximum extension in the spring is given by Xmax=2mω2lK−mω2
The maximum value of contact force between the bead and the rod is greater than mg
The correct Answer is:A, C, D
At equilibrium forces balance m(l+x)ω2=Kξmpliesx=mlω2K−mω2
Also till this point by work energy theorem x∫0m(l+x)ω2dx−Kx22=12mv2
V=√ml2ω4K−mω2
and at maximum elongation velocity becomes zero apply above concept of work & energy from start to zero velocity.
Topper's Solved these Questions
Similar Questions
A vertical rod is rotating about its axis with a uniform angular speed ω . A simple pendulum of length l is attached to its upper end what is its inclination with the rod ?
View SolutionA rigid mass less rod of length L is rotating in a vertical plane about a horizontal axis passing through one of its ends. At the other end of the rod there is a mass less metal plate welded to the rod. This plate supports a heavy small bead that can slide on the rod without friction. Just above the bead there is another identical metal plate welded to the rod. The bead remains confined between the plates. The gap between the plates is negligible compared to L. The angular speed of the rod when the bead is at lowest position of the circle is ω=2√gL. How many times a clink of the bead hitting a metal plate is heard during one full rotation of the rod ?

View Solution
Knowledge Check
AB is a light rigid rod. Which is rotating about a vertical axis passing through A,A spring of force constant K and natural length l is attached at A and its other end is attached to a small bead of mass m. The bead can slide without friction on the rod. At the initial moment the bead is at rest (w.rt. the rod) and the spring is unstreached Select correct option
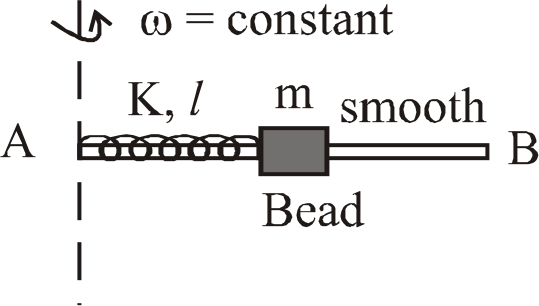 AThe maximum velocity attained by the bead w.r.t the rod is given by Vmax=√mω4l2K−mω2BThe maximum velocity attained by the bead w.r.t the rod is given by Vmax=√(mω4+Kmω2−K)ω2l2CThe maximum extension in the spring is given by Xmax=2mω2lK−mω2DThe maximum value of contact force between the bead and the rod is greater than mg
AThe maximum velocity attained by the bead w.r.t the rod is given by Vmax=√mω4l2K−mω2BThe maximum velocity attained by the bead w.r.t the rod is given by Vmax=√(mω4+Kmω2−K)ω2l2CThe maximum extension in the spring is given by Xmax=2mω2lK−mω2DThe maximum value of contact force between the bead and the rod is greater than mgA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
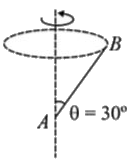 Aml23Bml24Cml216Dml212
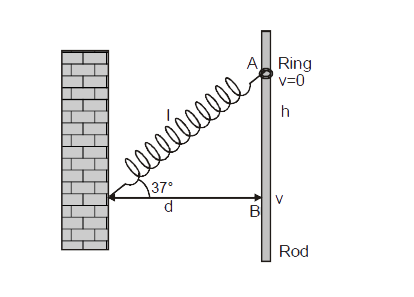
Aml23Bml24Cml216Dml212One end a light spring of natural length d and spring constant k(=mg/d) is fixed on a rigid support and the other end is fixed to a smoth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the support. Initially , the spring makes an angle of 37∘ with the horizontal as shown in the figure. The system is released from rest. The speed of the ring at the same angle subtended downward will be
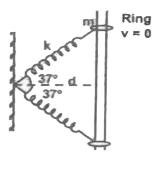 A√2gdB√3gdC√4gdD√gd/2
A√2gdB√3gdC√4gdD√gd/2

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
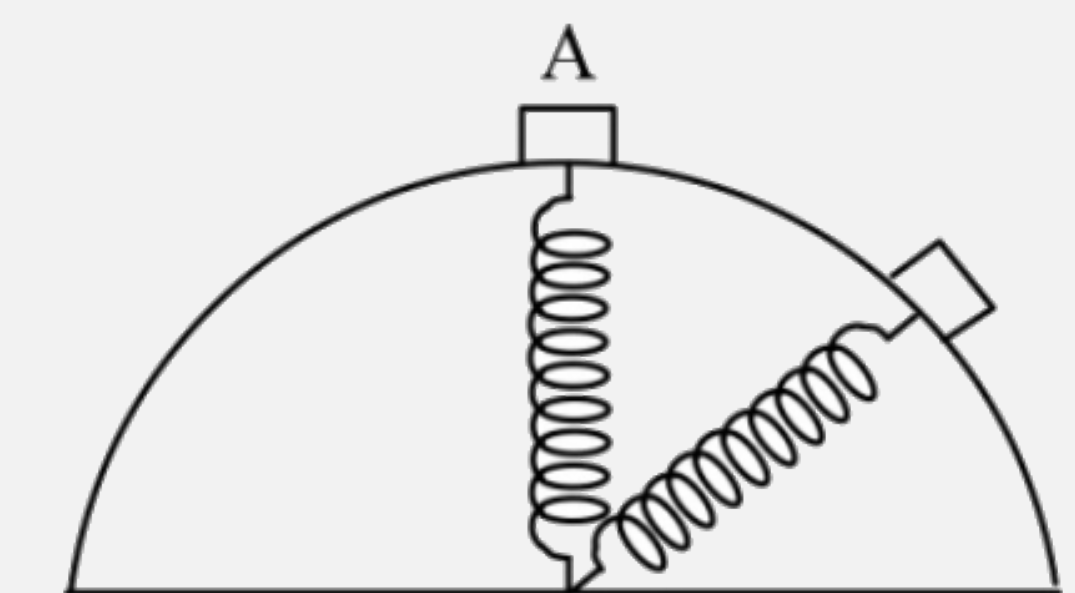
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
View SolutionA smooth light horizontal rod AB can rotate about a vertical axis passing through its end A. The rod is fitted with a small slieeve of mass m attached to the end A by a weightless spring of length l0 and stiffness x. What work must be performed to slowly get this system going and reaching the angular velocity ω?
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View Solution

