A bead of mass 5 kg is free to slide on the horizontal rod AB. They are connected to two identical springs of natural length h ms. As shown. If initially bead was at O & M is vertically below L then, velocity of bead at point N will be :

None of these
The correct Answer is:A
Step by step video, text & image solution for A bead of mass 5 kg is free to slide on the horizontal rod AB. They are connected to two identical springs of natural length h ms. As shown. If initially bead was at O & M is vertically below L then, velocity of bead at point N will be : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolvedMCQ
78 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question
31 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
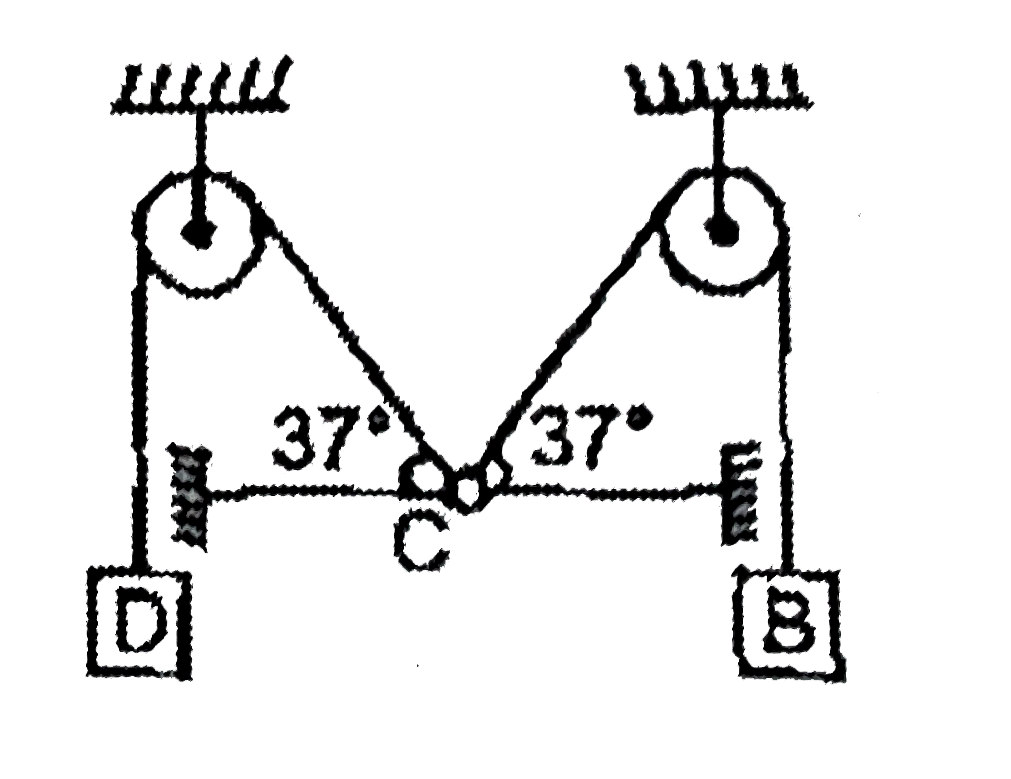
A bead C can move freely on a horizontal rod. The bead is connected by blocks B and D by a string as shown in the figure. IF the velocity of B is v. find the velocity of block D.
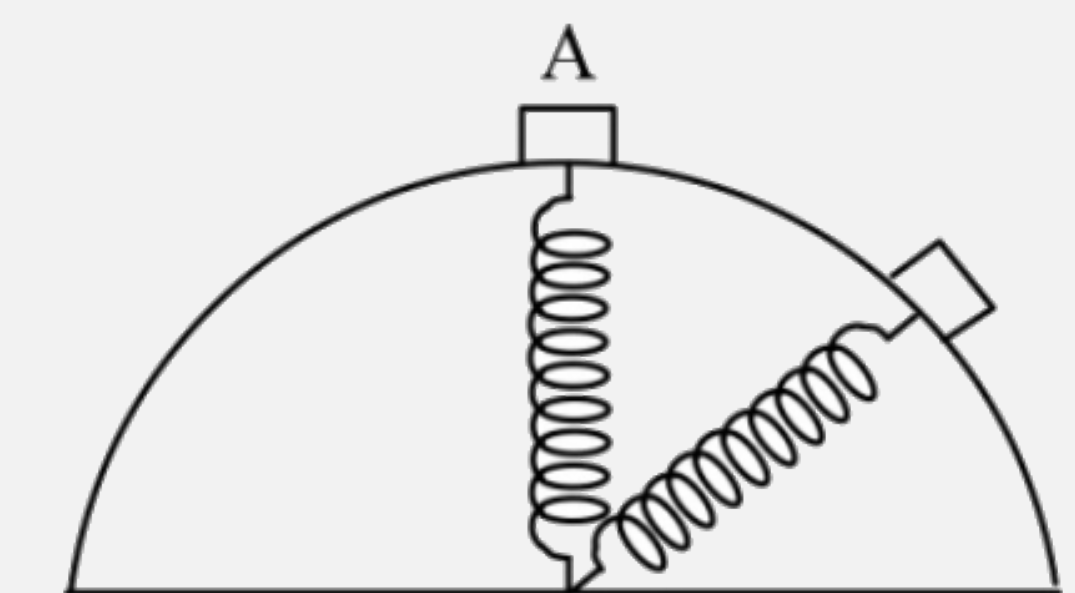
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View Solution
Knowledge Check
A bead B of mass 'm' can travel without frictionn on a smooth horizontalwire xx′. The bead is connected to a block of identical mass by an ideal string passing over an ideal pulley. The system, as shown, is in vertical plane.

System is initially released from rest in the position shown. Initial acceleration of block A is:AzeroBg2C3g7D4g7A bead B of mass 'm' can travel without frictionn on a smooth horizontalwire xx′. The bead is connected to a block of identical mass by an ideal string passing over an ideal pulley. The system, as shown, is in vertical plane.

The system is allowed to fall. Find the speed of block A at the instant when string connected to the bead B makes an angle 37∘ with vertical.A√agB√5ag17C√27ag68D√ag2In the shown figure two beads slide along a smooth horizontal rod as shown in figure. The relation between v and v0 in the shown position will be
 Av=v0cotθBv=v0sinθCv=v0tanθDv=v0cosθ
Av=v0cotθBv=v0sinθCv=v0tanθDv=v0cosθ
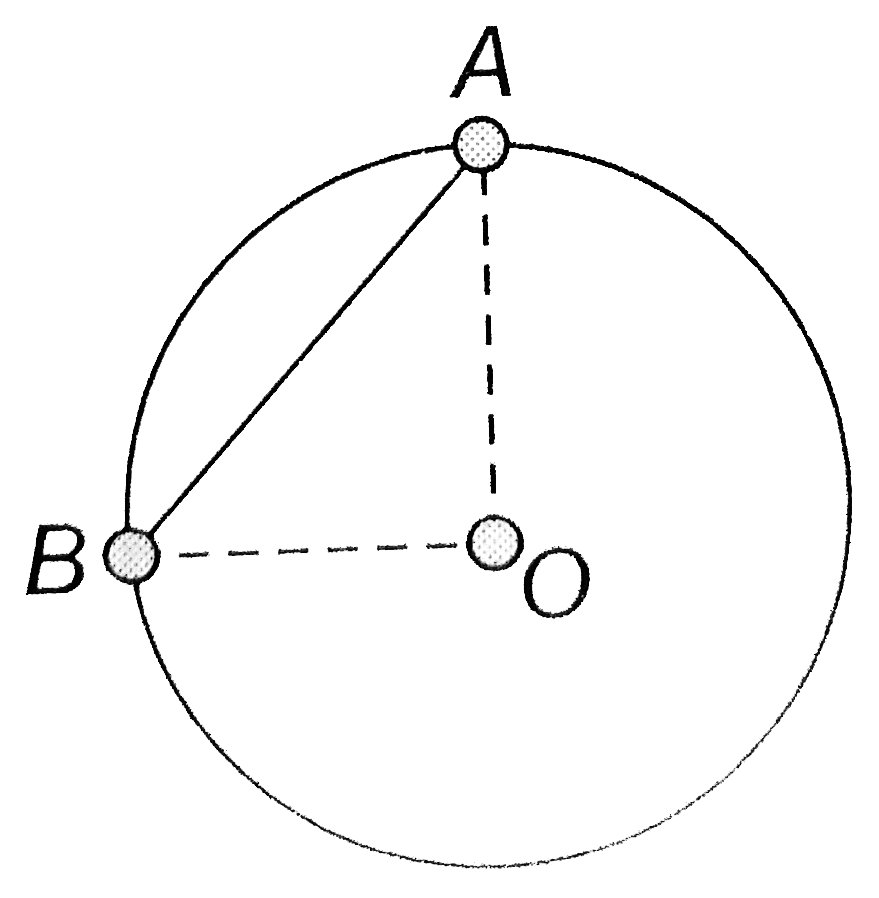
Beads A and B each of mass m , are connected by a light inextensible cord. They are constrained (restricted) to move on a frictionless ring in a vertical plane as shown. The beads are released from rest at the position shown. The tension in the cord just after the release is.
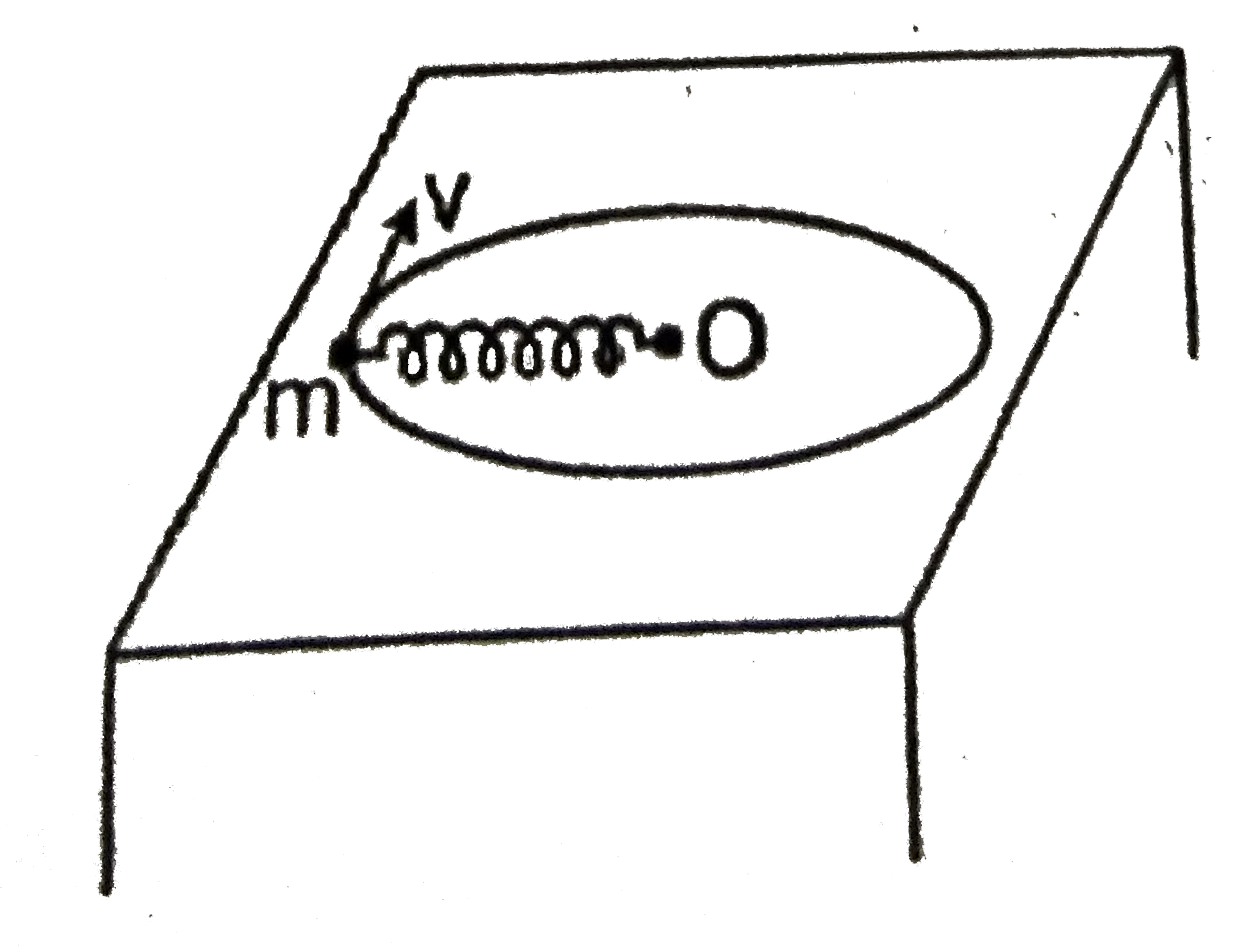
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionA bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is

View SolutionA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
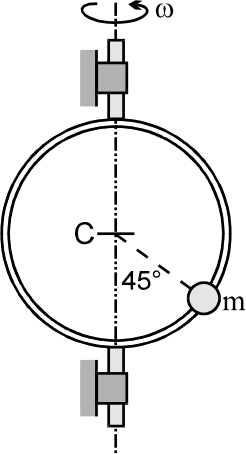
View SolutionA small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
View Solution
