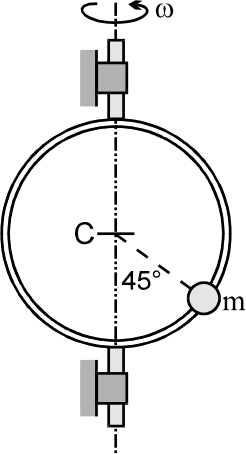
A small bead of mass m = 1 kg is free to move on a circular hoop. The circular hoop has centre at C and radius r = 1 m and it rotates about a fixed vertical axis. The coefficient of friction between bead and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop, at the position shown in figure is : (Take g=10m/s2)
(5√2)1/2
(10√2)1/2
(15√2)1/2
(30√2)1/2
The maximum angular speed of the hoop corresponds to the situation when the bead is just about to slide upwards. The free body diagram of the bead is

For the bead not to slide upwards.
mω2(rsin454∘)cos45∘−mgsin45∘<μN.....(1)
where N=mgcos45∘+mω2(rsin45∘)sin45∘......(2)
From 1 and 2 we get.
ω=√30√2rad/s
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionA hoop of radius r and mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases ot slip?
View SolutionA thin hoop of mass M and radius r is placed on a horizontal plane. At the initial instant, the hoop is at rest. A small washer of mass m with zero initial velocity slides from the upper point of the hoop along a smooth groove in the inner surfaces of the hoop. Determine the velocity u of the centre of the hoop at the moment when the washer is at a certain point A of the hoop, whose radius vector forms an angle ϕ with the vertical (figure). The friction between the hoop and the plane should be neglected

View SolutionA circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
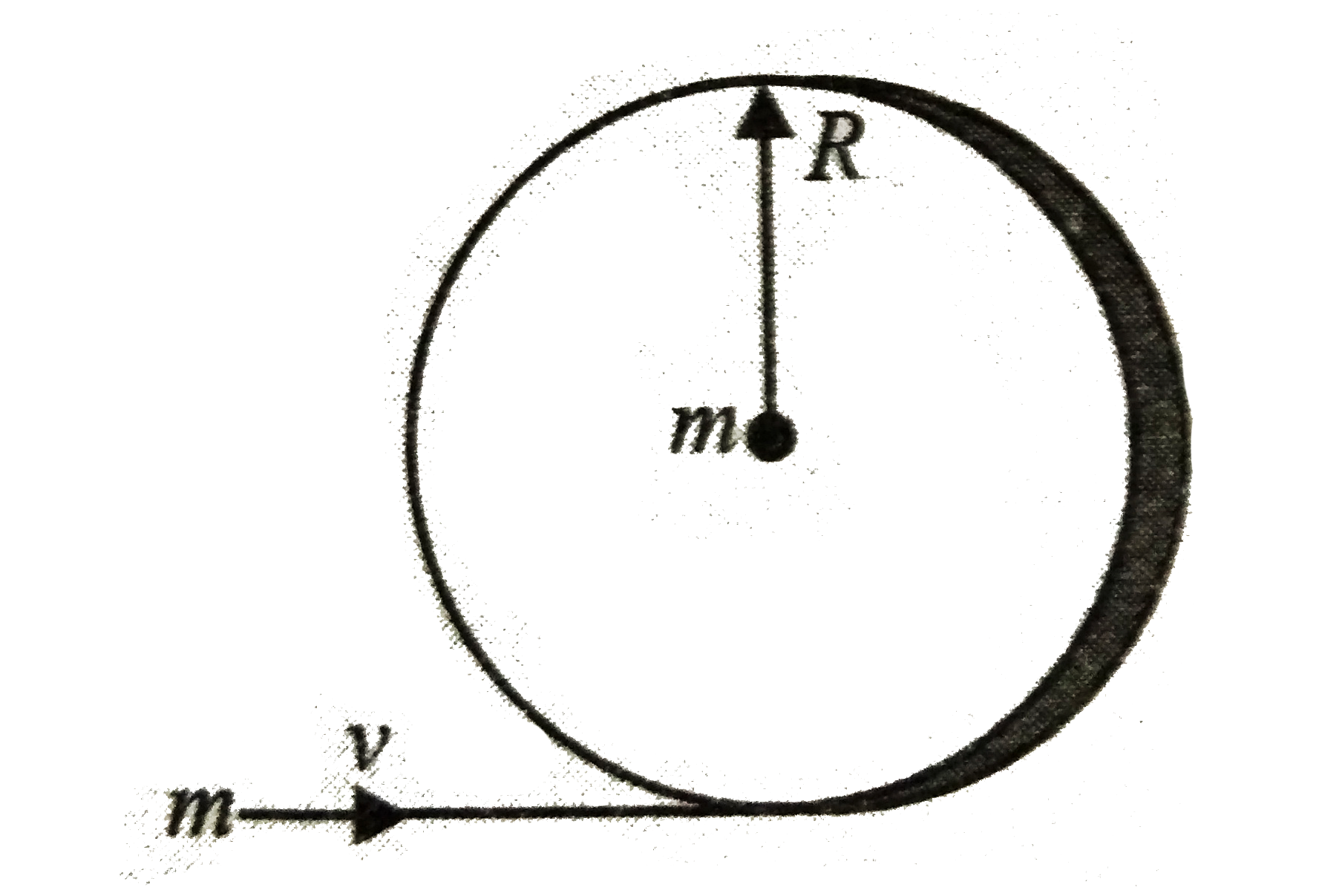
View SolutionA hoop of radius r mass m rotating with an angular velocity omega_(0) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Mark the correct option
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Velocity of bullet in ground frame, after collision is
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity upsilon strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop. Velocity of CM of hoop (ground frame)is
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity upsilon strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop. What is the impulse on bullet?
View SolutionA small bead of mass m is carried by a circular hoop having center at O and radius √2m which rotates about a fixed vertical axis. The coefficient of friction between beed and hoop is μ=0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop. (g=10m/s2)

View SolutionA bead of mass m slides without friction on a vertical hoop of radius R. The bead moves under the combined influence of gravity and a spring of spring constant k attached to the bottom of the hoop. For simplicity assume, the equilibrium length of the spring to be zero. The bead is released at the top of the hoop with negligible speed as shown . The bead, on passing the bottom point will have a velocity of :
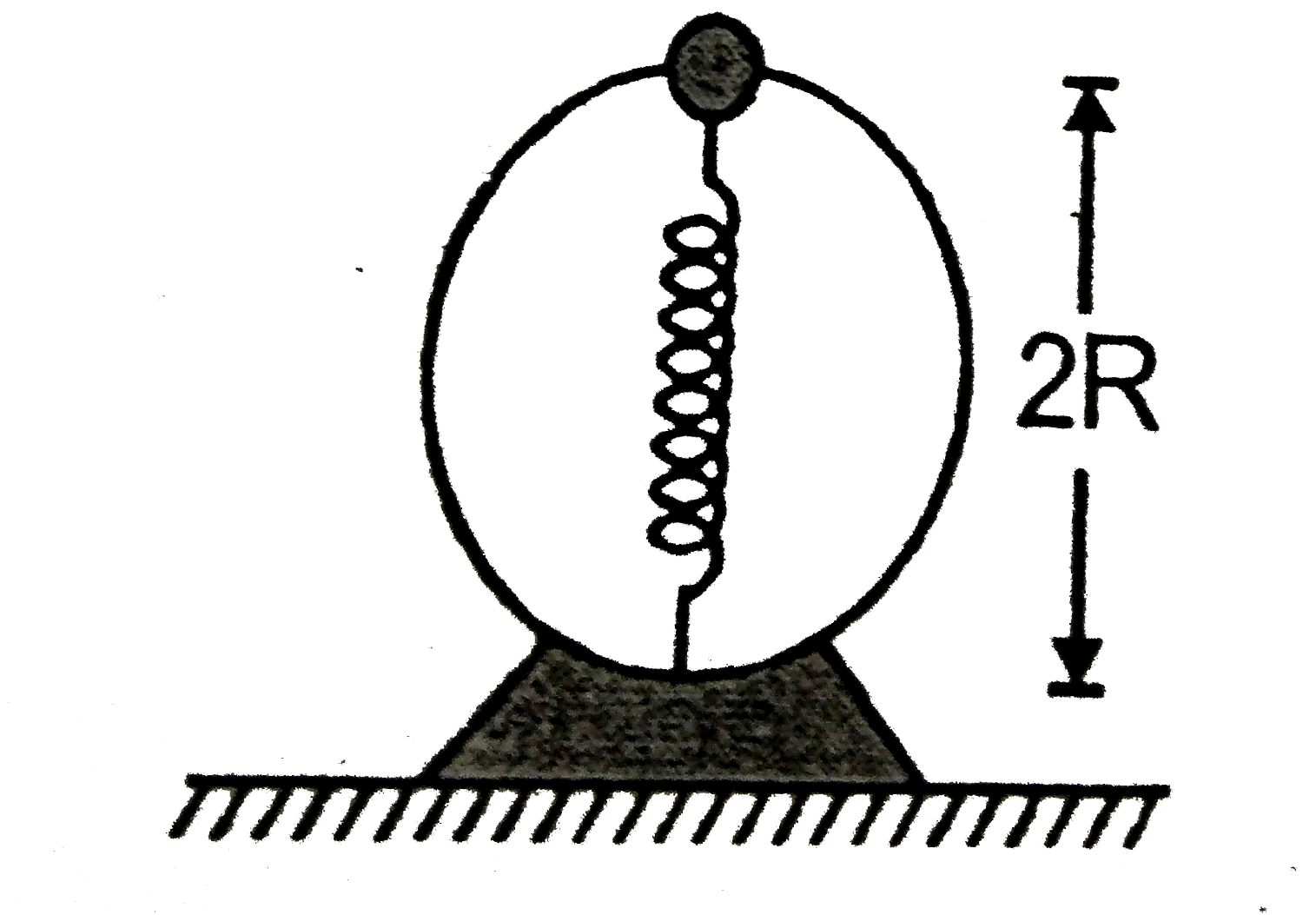
View SolutionA hoop of radius R rests on a horizontal surface. A similar hoop moves past it at a velocity v. Determine the velocity vA of the upper point of "intersection" of the hoops as a function of the distance d between their centres, assuming that the hoops are thin, and the second hoop is in contact with the first hoop as it moves past the latter.
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal frictionless surface A bullet also of mass m and moving with a velocity v strikes the hoop and gets embedded in it the thickness of the hoop is much smaller then R the angular velocity with which the system rotates after the bullet strikes the hoop is
View SolutionA hoop of radius r mass m rotating with an angular velocity omega_(0) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View Solution

