A circular wooden hoop of mass m and radius R rests fiat on a frictionless surface. A bullet, also of mass m and moving with a velocity v, strikes the hoop and gets embedded in it. The thickness of the hoop is much smaller than R. Find the angular velocity with which the system rotates in after the bullet strikes the hoop.
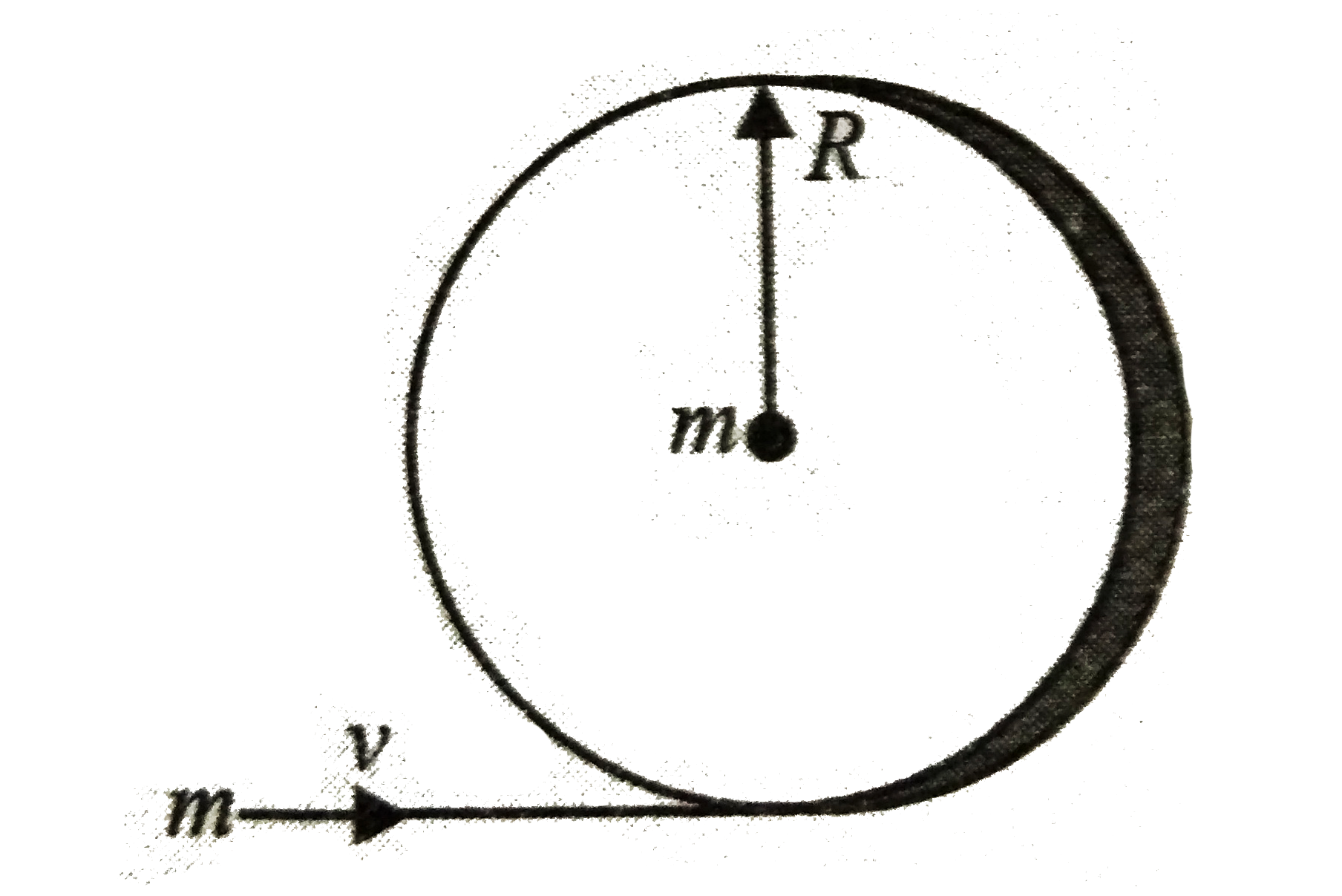
Let the velocity of the CM of the system after the strike be vc By conservation of linear momentum
Position of CM y=(m.O+m.R).((m+m))+m=R2
Using conservation of angular mometum about CM of the system (hoop+bullet).
mvR2Icω
=(Ibullet+Ihoop_(c)ω
=[m(R2)2+{mR2+m(R2)2}ω]
After solving we get ω=vR
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.3
Explore 21 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end. A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
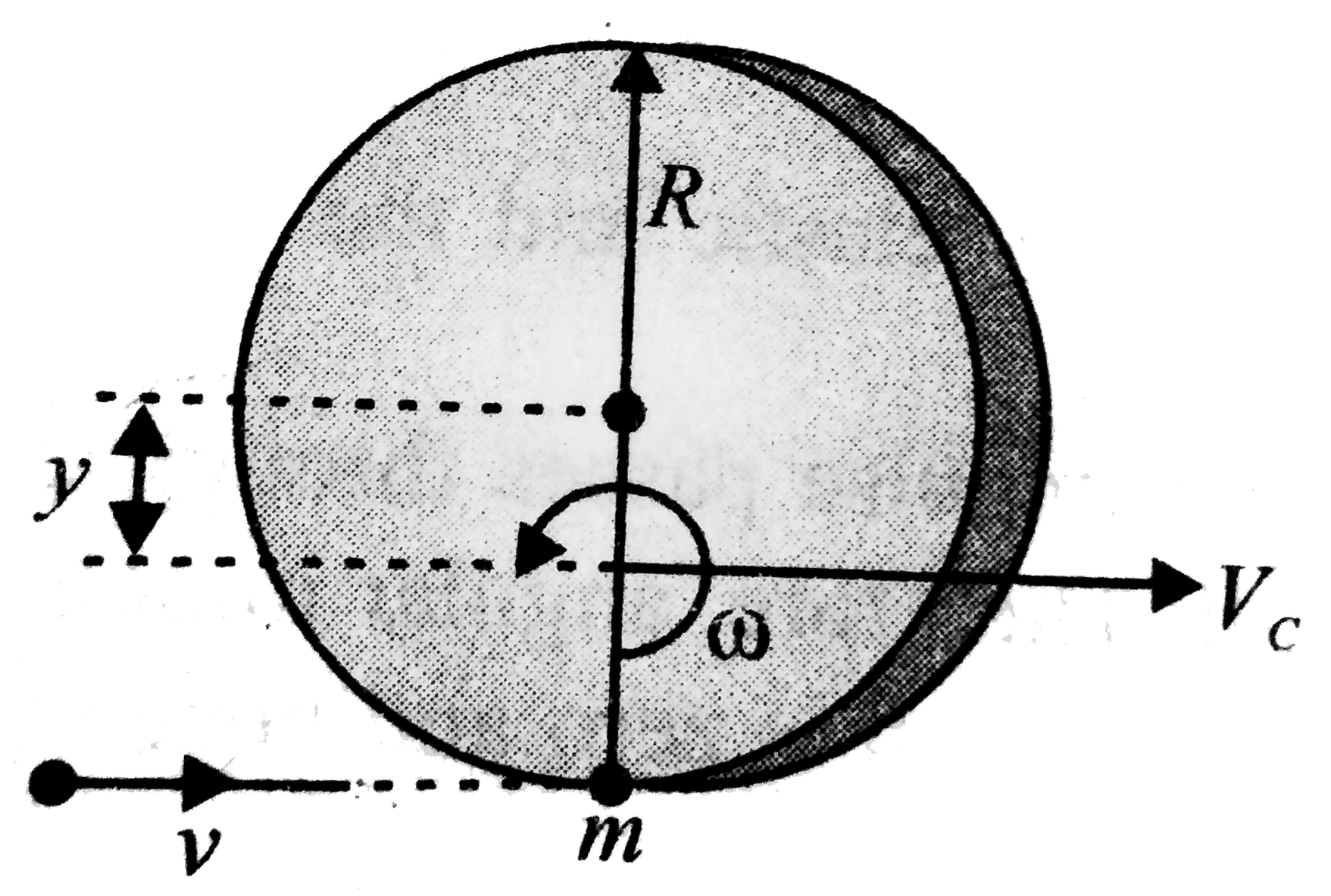
View SolutionA circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Velocity of CM of hoop (ground frame)is
View Solution
Knowledge Check
A circular hoop of mass m and radius R rests flat on a horizontal frictionless surface A bullet also of mass m and moving with a velocity v strikes the hoop and gets embedded in it the thickness of the hoop is much smaller then R the angular velocity with which the system rotates after the bullet strikes the hoop is
 AV/(4R)BV/(3R)C2V/(3R)D3V/(4R)
AV/(4R)BV/(3R)C2V/(3R)D3V/(4R)A circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Mark the correct optionAenergy of system (hoop+ bullet) is conservedBmomentum of system is conservedCangular momentum of system is conserved about any point in the plane of hoopDangular momentum is not conserved due to torque of gravitational force.A circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

What is the impulse on bullet?A−2μψlon03ˆiB−μψlon03ˆiCmυ0ˆiDmυ02ˆi
A circular hoop of mass m and radius R rests flat on a horizontal smooth surface. A bullet of same mass m and moving with velocity υ strikes the hoop tangentially and gets embedded in it. Neglect the thickness of hoop in comparision to radius of hoop.

Velocity of bullet in ground frame, after collision is
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View Solution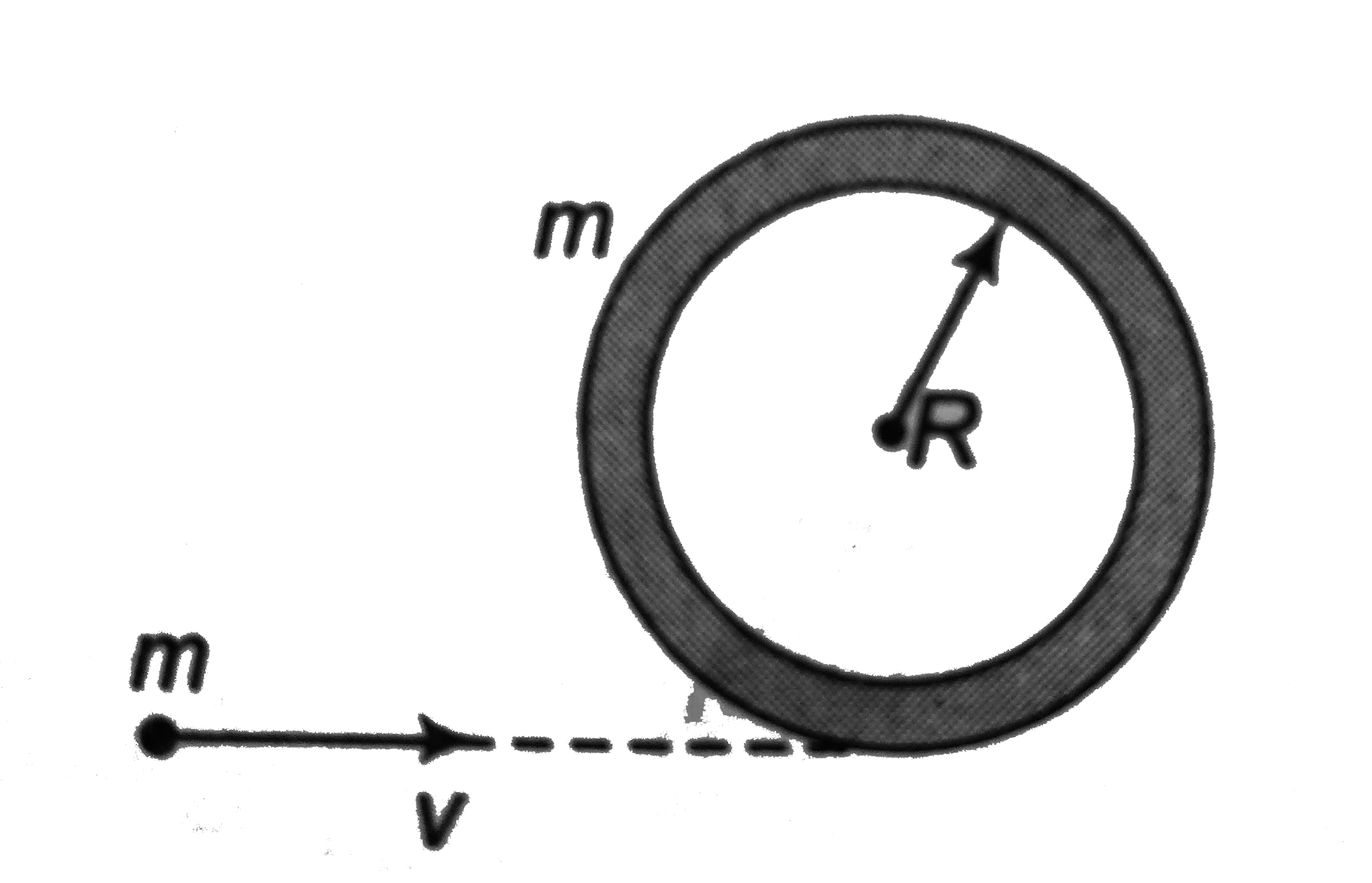
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View Solution

