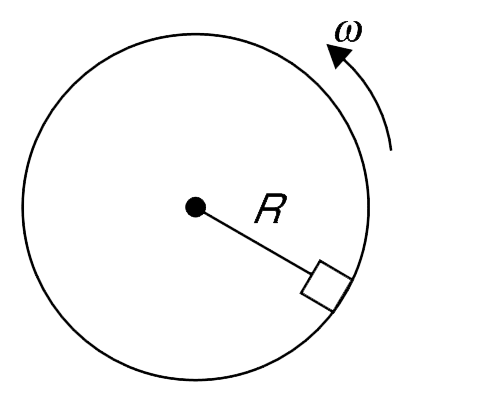
A cylinder of radius R is rotating about its horizontal axis with constant ω=√5gR. A block of mass m is kept on
the inner surface of the cylinder. Block is moving in vertical circular motion without slipping. co–efficient of friction between block and surface of cylinder is μ. If minimum value of μ for complete vertical circular motion of block is 2√63x then find 'x'.

N=mgcosθ+mω2R=mgcosθ+m(5gR)R⇒N=5mg+mgcosθ>0 so block does not leave circular motion
fr=maT for limiting case μN=maT⇒μ(mg(5+cosθ))=mgsinθ⇒μ=sinθ5+cosθ
dμdθ=(5+cosθ)(cosθ)−sinθ(−sinθ)(5+cosθ)2=0⇒cosθ=−15
μmax=√1−1255−15=2√624⇒x=8
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA block of mass m is kept on the edge of a horizontal turn table of radius R which is rotating with constant angular verticle omega (along with the block ) about its axis . If coefficient of friction is mu , find the friction force between block and table.
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical A small block kept in the bowl rotates with the bowl without slipping on its surface If the surface of bowl is smooth and angle made by radius through the block with the vertical is 0 find the angular speed at which the bowl is rotating .
View SolutionA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
View SolutionA cylinder with radius R spins about its horizontal axis with angular speed ω. There is a small block lying on the inner surface of the cylinder. The coefficient of friction between the block and the cylinder is μ. Find the value of ω for which the block does not slip, i.e., stays at rest with respect to the cylinder.
View SolutionA string wrapped around a cyliner of mass m and radius R . The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder. Acceleration of cylinder is:
View SolutionA string wrapped around a cyliner of mass m and radius R . The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder. Velocity of point of contact 'of cylinder at this moment is:
View SolutionA string wrapped around a cyliner of mass m and radius R. The end of the string is connected to block of same mass hanging vertically. No friction exists between the horizontal surface and cylinder.
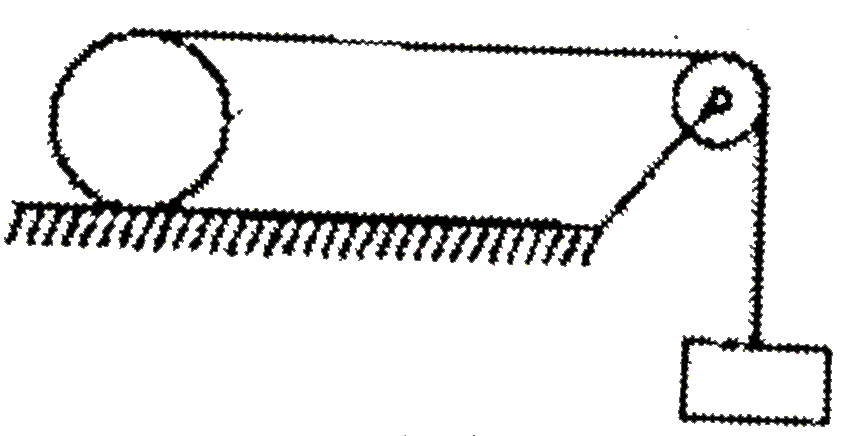
Velocity of hanging block at this moment is: is:
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity omega about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction mu. A force is applied to the block at an angle theta with the horizontal. The block will move with a minimum force F if
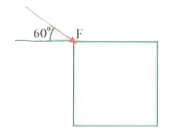
View SolutionA block of mass √3kg is kept on a frictional surface with μ=12√3. The minimum force to be applied as shown to move the block is
View SolutionA hemispherical bowl of radius R si set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA hollow vertical cylinder of radius R is rotated with angular velocity omega about an axis through its centre. What is the minimum coefficient of static friction between block M and cylinder wall necessary to keep the block suspended on the inside of the cylinder ?
View Solution

