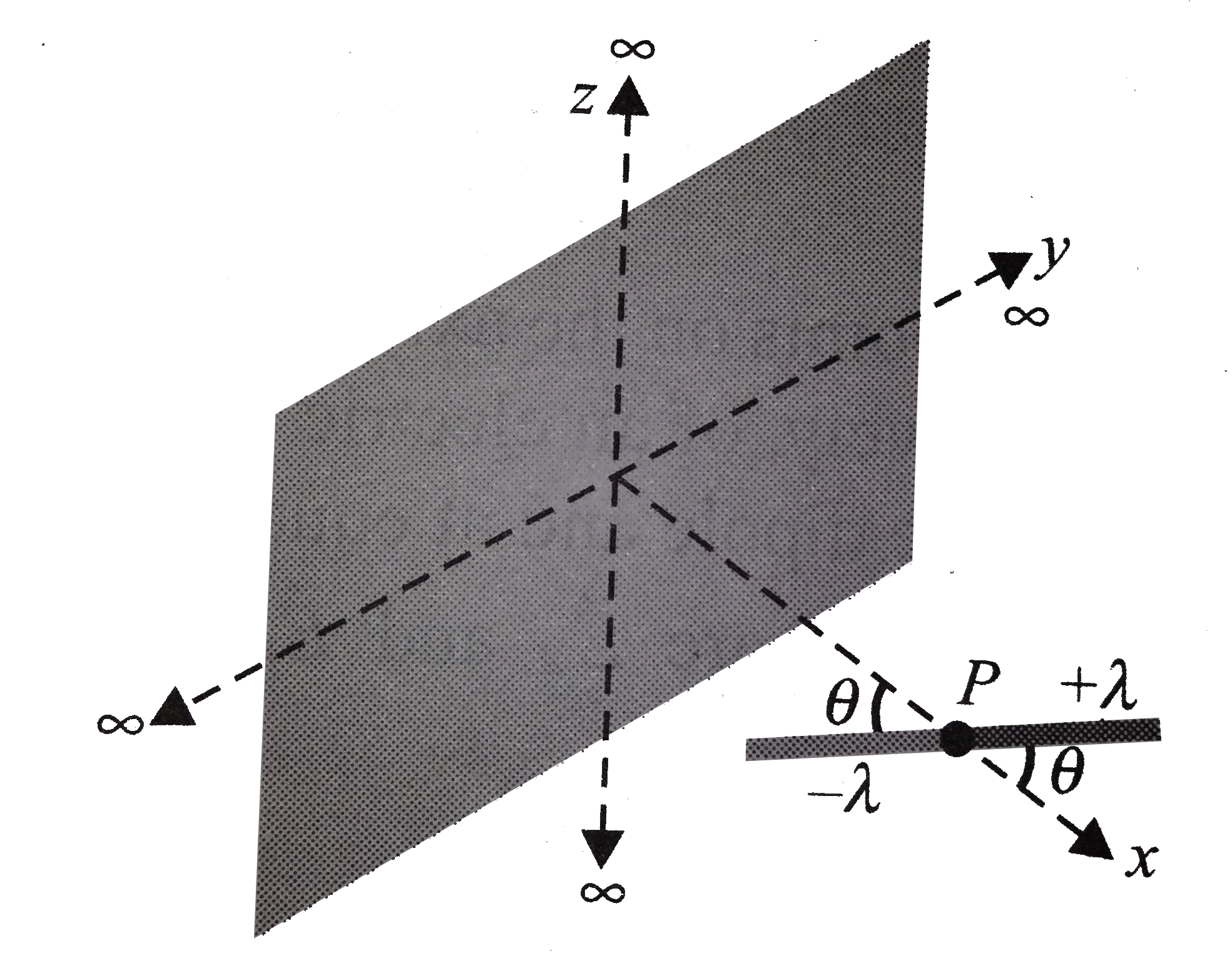
A large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
0
σλl22ɛ0sinθ
σλl2ɛ0sinθ
σλl2ɛ0
The correct Answer is:B
dtua=2∫l0dFx.sinθ=2∫l0=2∫−0lE.dqxsinθ
=2E∫l0dxsinθ
(##NGPHYC01E01046_S01.png width=80%><br> = 2 lambda E sin theta int_0^l x dx = 2 lambda E sin theta. [x^2/2]_0^l<br> =lambda E sinq.l^2 = (sigma lambdal^2)/(2 in_0) sin theta.
Similar Questions
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its mid point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released.
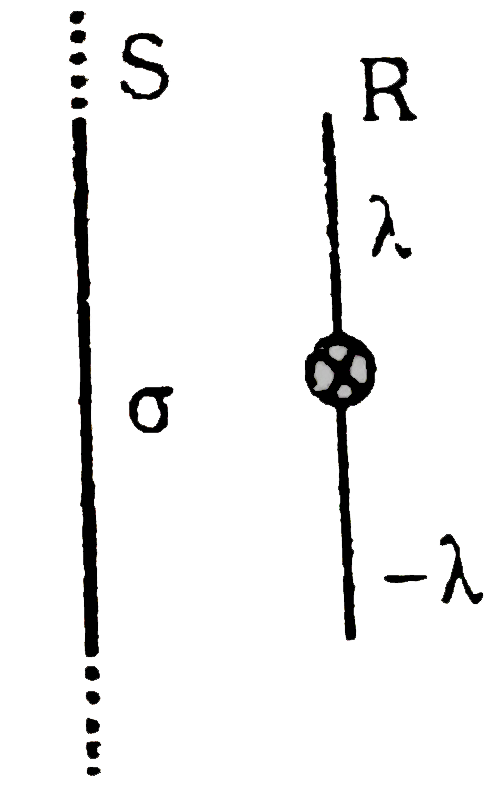
View SolutionIn the figure shown, S is a large non-conducting sheet of uniform charge density σ. A rod R of length I and mass m is parallel to the sheet and hinged at its midpoint. The linear charge densities on the upper and lower half of the rod are shown in the figure. The angular acceleration of the rod just after it is released is pσλqmɛo. Find pq.
'(##CEN_KSR_PHY_JEE_C18_E01_031_Q16##)'
View Solution
Knowledge Check
A half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
Aλ4εoln0Bλ4π2ε0rCλ4πε0rDλ4πε0r2A ring carries a uniform linear charge density on one half and the linear charge density of same magnitude but opposite sign on the other half.
AThe component of electric field along the axis at all points on the axis is zeroBthe electric field along the axis and on the axis is zero only at the centreCthe resultant field at the centre is zeroDthe resultant field at all points on the axis is zero
In the figure shown S is a large nonconducting sheet of uniform charge density σ. A rod R of length l and mass 'm' is parallel to the sheet and hinged at its point. The linear charge densities on the upper and lower half of the rod are shown in the figure. Find the angular acceleration of the rod just after it is released
[3σλ2m∈0]
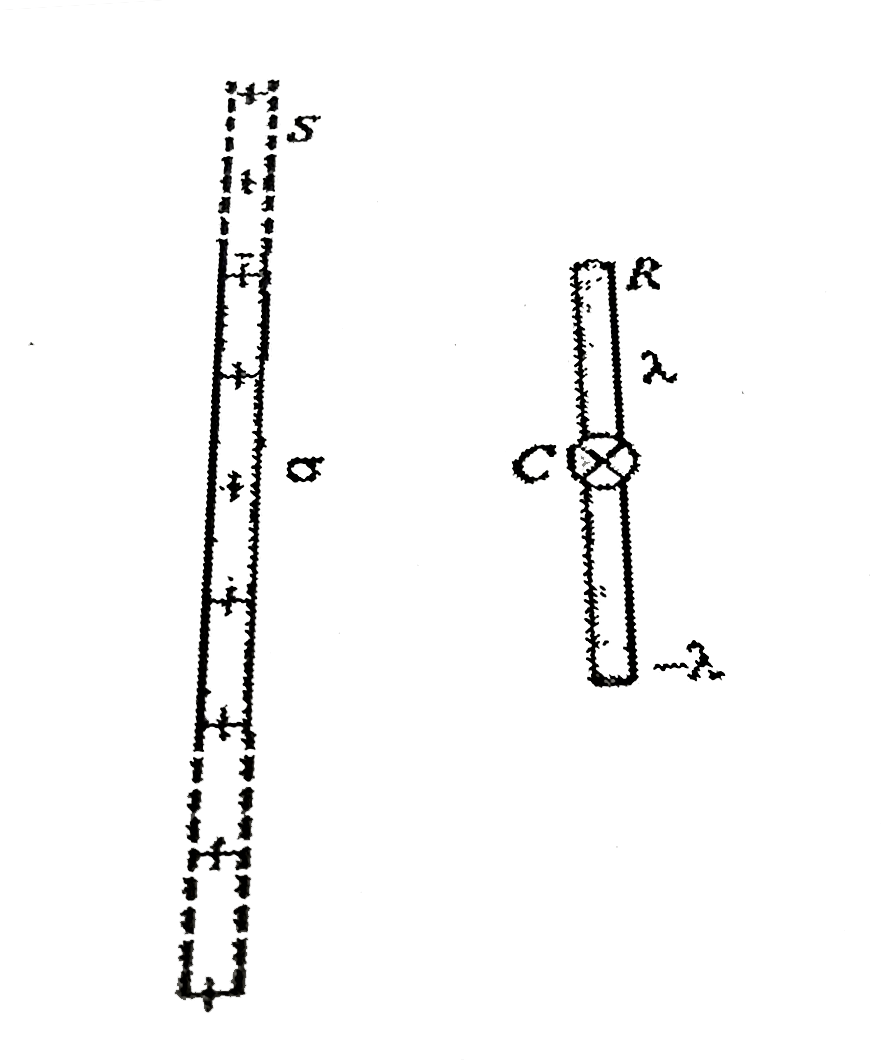
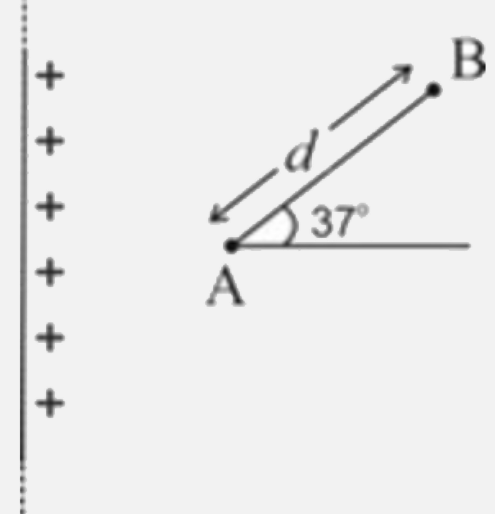
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.

View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionYou are given a rod of length L. The linear mass density is λ such that λ=a+bx. Here a and b are constants and the mass of the rod increases as x decreases. Find the mass of the rod

View SolutionAn insulting thin rod of length l has a linear charge density ρ(x)=ρ0xl on it. The rod is rotated about an axis passing through the origin (x=0) and perpendicular to the rod. If the rod makes n rotations per second, then the time averaged magnetic moment of the rod is :
View Solution