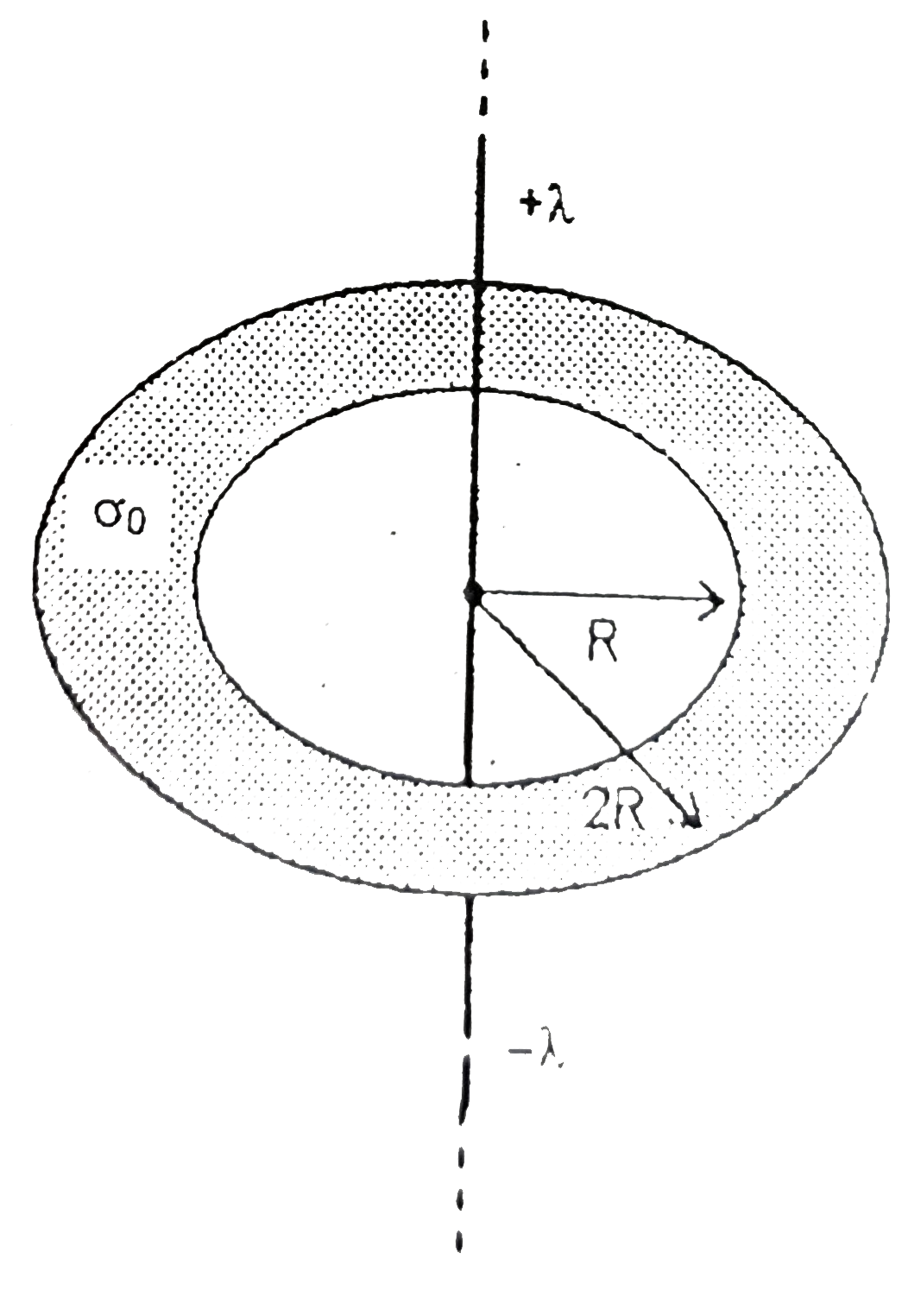
A non conducting infinite rod is placed along the $z -$ axis the upper half of the rod (lying along $z \geq 0$ ) is charged positively with a uniform linear charge density $+ λ$ , while the lower half ( $z < 0$ ) is charged negatively with a uniform linear charge density $- λ$ . The origin is located at the junction of the positive and negative halves of the rod. A uniformly charged annular disc (surface charge density : $σ_{0}$ ) of inner radius $R$ and outer radius $2 R$ is placed in the $x - y$ plane with its centre at the origin. find the force on the rod due to the disc.

$\frac{2 σ_{0} λ R}{ε_{0}}$

$\frac{σ_{0} λ R}{2 ε_{0}}$

$\frac{σ_{0} λ R}{ε_{0}}$

$\frac{σ_{0} λ R}{3 ε_{0}}$

Video Solution

Text Solution

Verified by Experts

The force on the rod due to the annular disc is equal and opposite to that on the disc due to the rod. We take an annular strip of radius $r$ and width $d r$ and find the force acting on it
$d F = (σ_{0} 2 π r d r) \frac{λ}{2 π ε_{0} r} = \frac{λ σ_{0}}{ε_{0}} d r$
$∴$ The force
$F = \frac{σ_{0} λ}{ε_{0}} \int_{R}^{2 R} d r = \frac{σ_{0} λ R}{ε_{0}}$

Updated on:21/07/2023

The dimensional formula of linear charge density $λ$ is
A $[M^{- 1} L^{- 1} T^{+ 1} A]$
B $[M^{0} L^{- 1} T^{+ 1} A]$
C $[M^{- 1} L^{- 1} T^{+ 1} A^{- 1}]$
D $[M^{0} L^{- 1} T^{+ 1} A^{- 1}]$
A half ring of radius $r$ has a linear charge density $λ$ .The potential at the centre of the half ring is
A $\frac{λ}{4 ε o {ln}_{0}}$
B $\frac{λ}{4 π^{2} ε_{0} r}$
C $\frac{λ}{4 π ε_{0} r}$
D $\frac{λ}{4 π ε_{0} r^{2}}$
If linear charge density of a wire as shown in the figure is $λ$

Apotential at the centre is $\frac{λ}{2 ε_{0}}$
Belectric field at the centre of the loop is $\frac{λ}{2 π ε_{0} R}$
Celectric field at the centre of the loop is $\frac{λ}{2 π ε_{0} R} + \frac{λ}{2 ε_{0} R}$
DNone of the above