A metallic disc of radius r is made of a material of negligible resistance and can rotate about a conducting horizontal shaft. A smaller non conducting disc of radius a is fixed onto the same shaft and has a massless cord wrapped around it, which is attached to a small object of mass m as shown. Two ends of a resistor of resistance R are connected to the perimeter of the disc and to the shaft by sliding contacts. The system is then placed into a uniform horizontal magnetic field B and the mass m is released. Find the terminal angular velocity with which the disc will rotate finally.
(Take r=10cm, a=2cm, R=1100Ω, B=0.2T, m=50gm, g=10m/s2)

200rad/s
300rad/s
100rad/s
10rad/s
At terminal stage, torque applied on the smaller disc by the rope =mga
current to the disc =Bωr22R(where ω is terminal angular velocity)
torque applied by magnetic field =B2ωr44R
So, B2ωr44R=mga
ω=100rad/sec
Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
Knowledge Check
A disc of radius r is removed from the centre of a disc of mass M and radius R. The M.I. About the axis through the centre and normal to the plane will be:
AM(R2−r2)/2BM(R2+r2)/2CM(R4−r4)/2R2DM(R2)/2A uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
A2MM+2mgB2mM+2mgCM+2m2MgD2M+m2MgA uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
ATMRBMRTC2TMRDMR2T
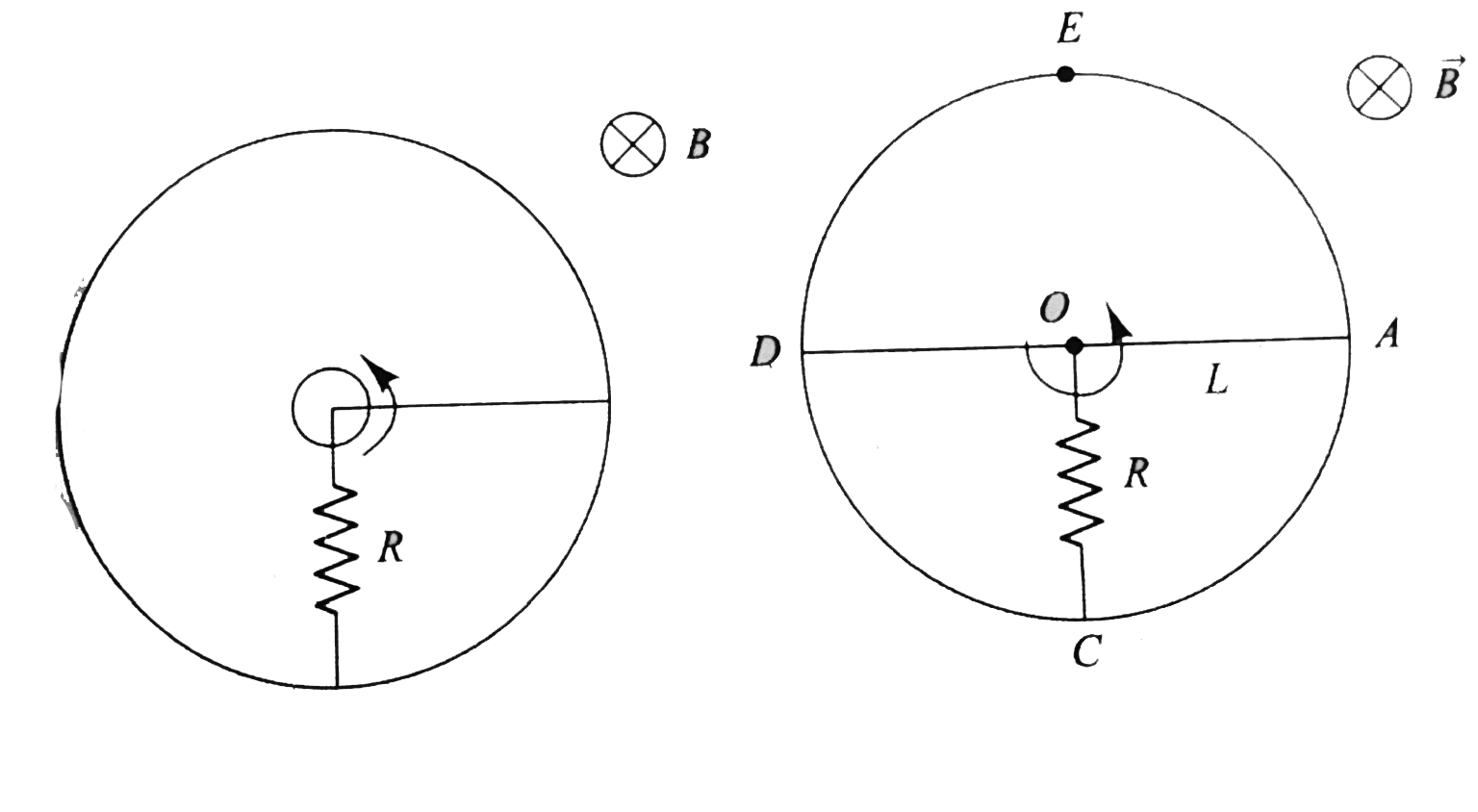
A rod of length l and resistance r rotates about one end as shown in figure.Its othr end touches a conducting ring a of negligible resistance.A resistance R is connected between centre and periphery.Draw the electrical equivalence and find the current in the resistance R.There is a uniform magnetic field B directed as shown.

View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system

View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system :

View SolutionA rod of length L and resistance r rotates about one end as shown in . Its other end touches a conducting ring of negligible resistence. A resistence R is connected between the center and periphery. Draw the electrical equivalence and find the current in resistance R. There is a uniform magnetic field B directed as shown in .
View SolutionFind moment of inertia of half disc of radius R2 and mass M about its centre. A smaller half disc of radius R1 is cut from this disc

View Solution