A sphere is moving towards the positive x-axis with a velocity vc and rotates clockwise with angular speed ω shown in Fig. such that vc>ωR. The instantaneous axis of rotation will be
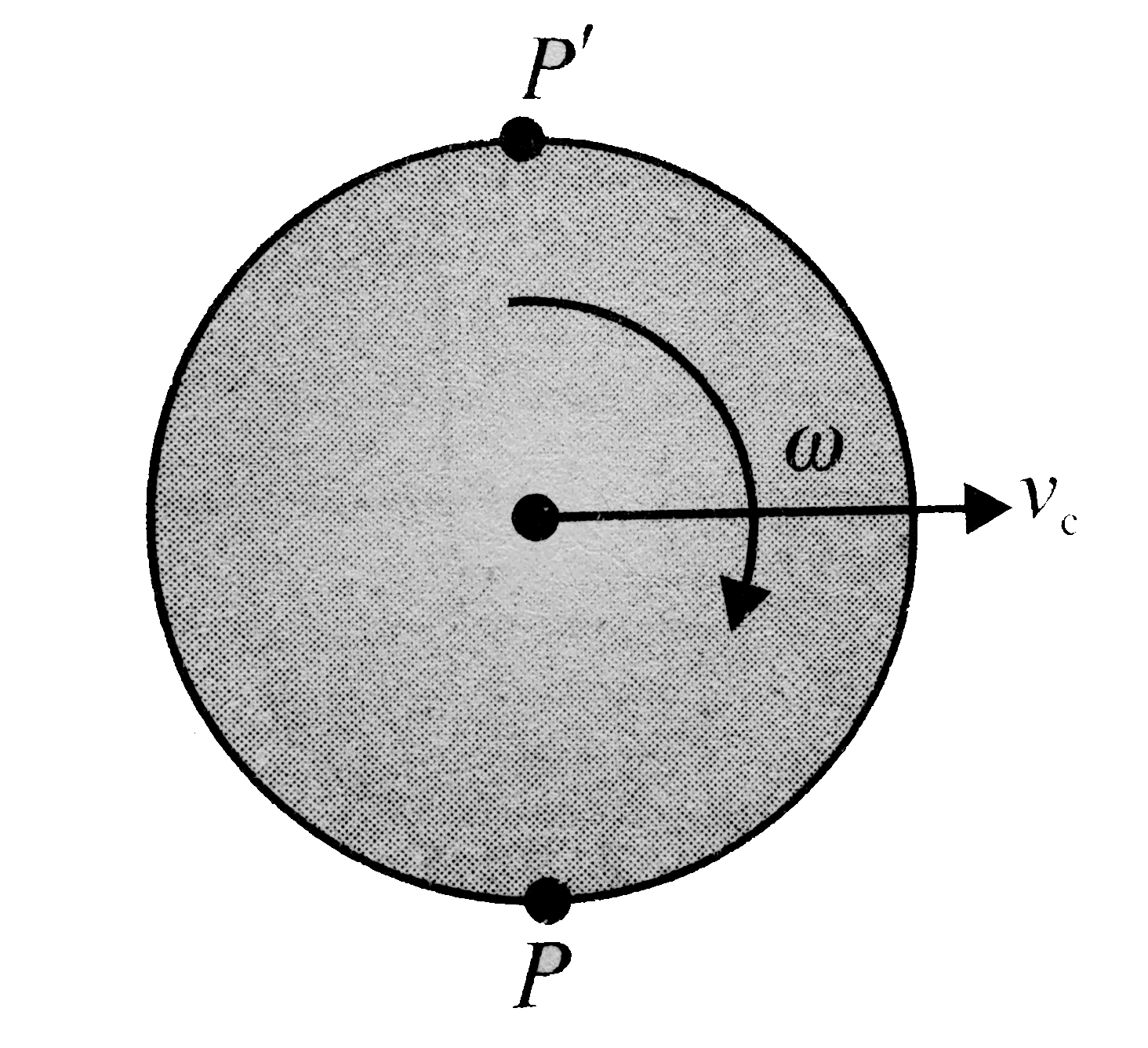
on point P
on point P'
inside the sphere
outside the sphere.
The instantaneous axis of rotation will fall on the outside of the sphere. Since in case of pure rotation, instantaneous axis of rotation will be on the centre. In case of pure rolling, instantaneous axis of rotation will be on P.
But if vc>ωR, so instantaneous axis of rotation will fall out of the sphere.

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question
58 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based
61 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
Knowledge Check
A sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
Aat the bottom of the sphereBat the top of the sphereCat the centre of the sphereDanywhere inside the sphereA rod of length l is travelling with velocity v and rotating with angular velocity ω such that ωl2=v. The distance travelled by end B of the rod when rod rotates by an angle π2 is
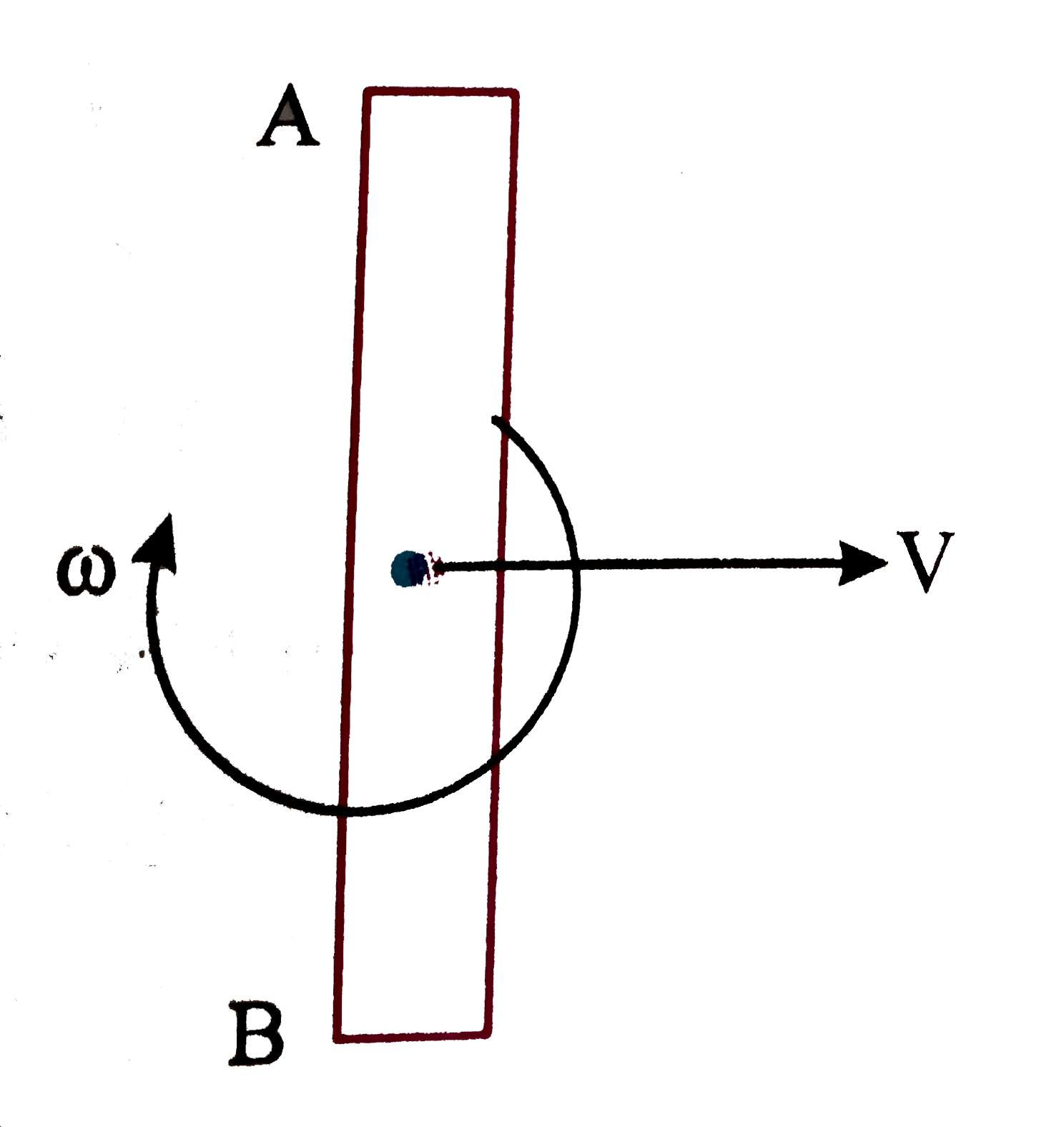 A√2(2)lB52lC3lD4l
A√2(2)lB52lC3lD4lA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2

A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
View SolutionA disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then

View SolutionA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
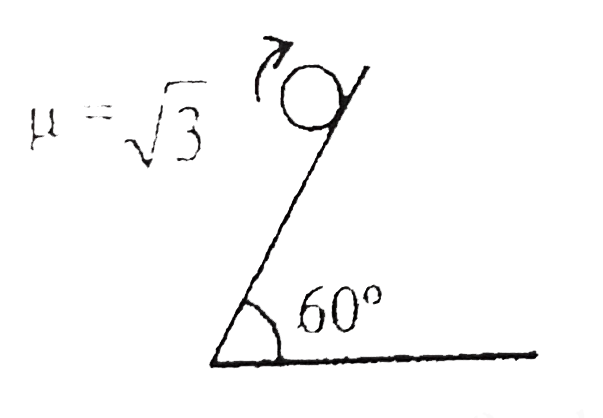
View SolutionA rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
View SolutionA rod of length l is given two velocities v1 & v2 in opposite directions at its two ends at rigt angles to the length. The distance of the instantaneous axis of rotation from v1 is:
View Solution

