A sphere of mass m is rotated about its axis by an angular velocity $ω$ and lowered gently on an inclined plane as shown in figure. Then initally

A

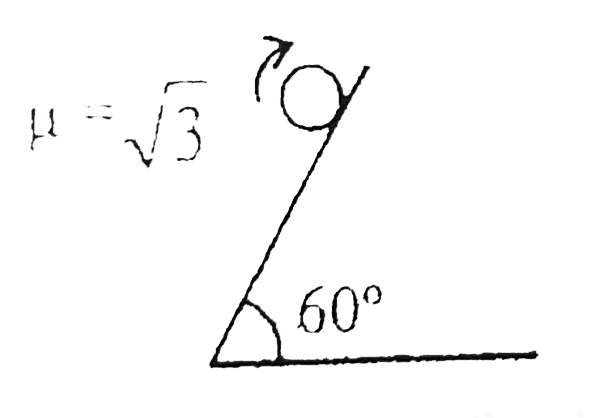
the centre of mass of sphere accelerates upwards.

B

the centre of mass of shpere accelerates downwards

C

the lowest point of contact accelerates upwards.

D

the lowest point of contect accelerates downwards.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$m g sin θ - f = m a$
$mg \frac{\sqrt{3}}{2} - μ m g {cos 60}^{\circ} = m a$

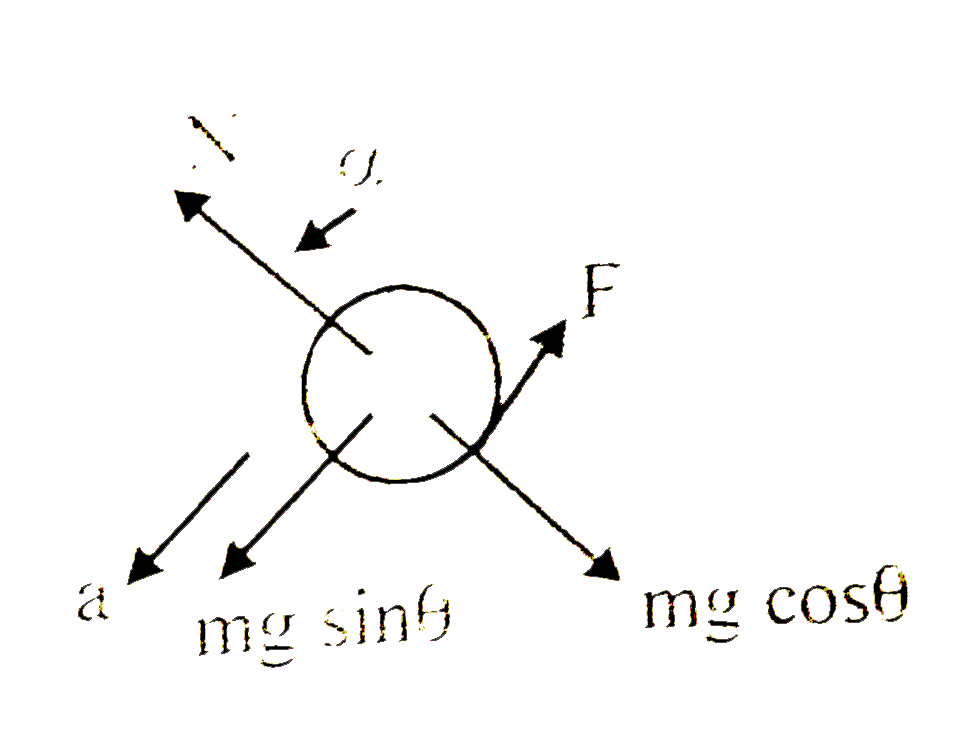
$mg \frac{\sqrt{3}}{2} - \frac{\sqrt{3}}{2} m g = m a$
$a = 0$
$τ_{C O M} \Rightarrow f R = I α$
$α = \frac{f R}{I}$
a point contact is towards up the plane.

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An cylinder of mass $m$ is rotated about its axis by an angular velocity $ω$ and lowered gently on an inclined plane as shown in figure. Then :
.
Ait will start going upward
Bit will first going upward and then downward
Cit will go downward just after it is lowered
Dit can never go upward.
Question 2 - Select One
A disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then

AIt will rotate at the position where it was placed and then will move downwards
BIt will go downwards just after it is lowered
CIt will go downwards first and then climb up
DIt will climb upwards and then move downwards
Question 3 - Select One
A non-conducting disk of radius $R$ is rotating about its own axis with constant angular velocity $ω$ in a perpendicular uniform magnetic field $B$ as shown in figure. The emf induced between centre and rim of disk is

A $\frac{B ω R^{2}}{2}$
B $B ω R^{2}$
CZero
D $\frac{B ω R^{2}}{3}$

BANSAL-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile